Tập xác định : D= R\ {-2}.
Lấy x 1 ≠ x 2 , khi đó ta có:
f x 2 - f x 1 x 2 - x 1 = m x 2 + 2 - m x 1 + 2 x 2 - x 1 = m x 1 + 2 - m x 2 + 2 x 2 + 2 . x 1 + 2 x 2 - x 1 = m x 1 - x 2 x 2 + 2 x 1 + 2 x 2 - x 1 = - m x 2 + 2 x 1 + 2
Với x 1 ; x 2 thuộc - 2 ; + ∞ hoặc cùng thuộc - ∞ ; - 2 thì x 1 + 2 x 2 + 2 > 0
Vì vậy f(x) nghịch biến khi f x 2 - f x 1 x 2 - x 1 < 0 ⇔ - m < 0 ⇔ m > 0 .
Tìm m để hàm số y = x − 2 m + 3 x − m + 3 x − 1 − x + m + 5 xác định trên khoảng (0; 1)
A. m ∈ 1 ; 3 2
B. m ∈ − 3 ; 0
C. m ∈ − 3 ; 0 ∪ 0 ; 1
D. m ∈ − 4 ; 0 ∪ 1 ; 3 2
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
Cho hàm số: y = m x x − m + 2 − 1 với m là tham số. Tìm m để hàm số xác định trên (0; 1)
A. M ∈ ( − ∞ ; 3 2 ] ∪ { 2 }
B. M ∈ ( − ∞ ; - 1 ] ∪ { 2 }
C. M ∈ ( − ∞ ; 1 ] ∪ { 3 }
D. M ∈ ( − ∞ ; 1 ] ∪ { 2 }
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
Tìm m để hàm số \(y=\sqrt{x-m}+\frac{1}{\sqrt{2m-3-x}}\) xác định trên khoảng (0, 1 )
Mọi người giúp mk mấy bài trong ảnh vs thêm 3 câu trắc nghiệm này nhé( gkhi ghi đáp án trắc nghiệm, giải thích rõ giúp mk vs nhé!!!!!)
1. Tìm m để hàm số y=2x/(x-m) xác định với mọi x thuộc (0;1)
A. m ≤ 0 ∨ m ≥ 1 B. m< 0 ∨ m>1
C. m<1 D. m>0
2. Cho 2 tập hợp: A=[2m-1; + ∞) ; B=(- ∞;m+3]. A ∩B khác 0 khi và chỉ khi:
A. m ≤4 B.m ≥3 C.m ≥-4 D. m ≥4
3. Cho 2 tập hợp: A=[-1;3] ; B=[m;m+5]. Để A ∩B=A thì m thuộc tập nào sau đây:
A.[-1;0] B.[-3;-2] C.[-2;-1] D.[1;2]
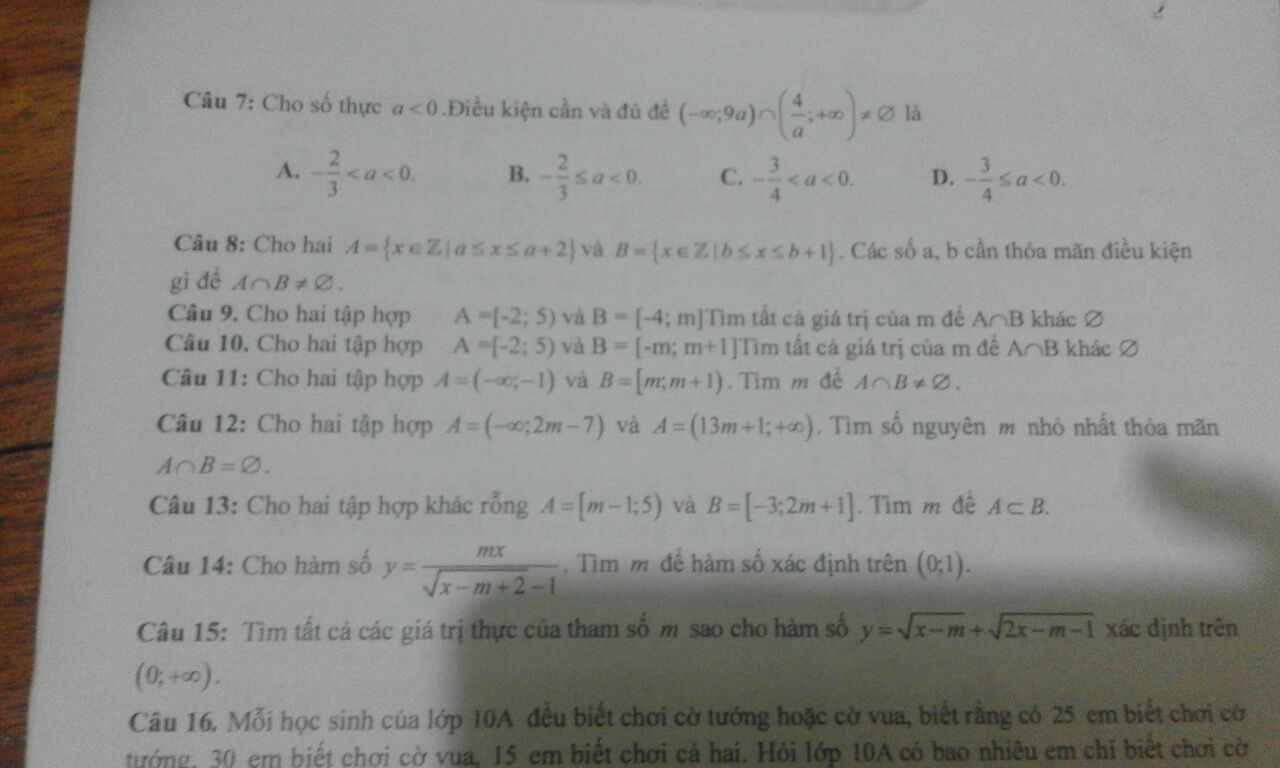GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
Tìm tất cả các giá trị thực của tham số m để hàm số y = − x 2 + (m−1)x + 2 nghịch biến trên khoảng (1; 2).
A. m < 5
B. m > 5
C. m < 3
D. m > 3
Tìm m để hàm số y = - 2x^2- (2m - 1)x + 6 - 3m nghịch biến trong khoảng (-2 ; dương vô cùng)
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 m + 2 x − m xác định trên (-1; 0)
A. m > 0 m < − 1
B. m ≤ − 1
C. m ≥ 0 m ≤ − 1
D. m ≥ 0
