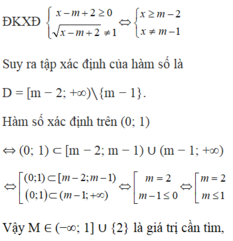Các câu hỏi tương tự
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
Hàm số \(\dfrac{x+2}{x-m+2}\) xác định trên (1; 3) khi:
A. m < 3 B. m ≥5 C. m < 3 hoặc m > 5 D. m ≥ 5 hoặc m ≤ 3.
cho hàm số y=x^2-3(m+1)x+m^2+3m-2, m là tham số . Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
+
2
m
+
2
x
−
m
xác định trên (-1; 0) A.
m
0
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 m + 2 x − m xác định trên (-1; 0)
A. m > 0 m < − 1
B. m ≤ − 1
C. m ≥ 0 m ≤ − 1
D. m ≥ 0
Tìm tất cả các giá trị thực của tham số mm để hàm số
y
x
−
m
+
2
x
−
m
−
1
xác định trên (0; +
∞
). A.
m
≤
0
B.
m
≥
1
C.
m
≤
1
D.
m
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số mm để hàm số y = x − m + 2 x − m − 1 xác định trên (0; + ∞ ).
A. m ≤ 0
B. m ≥ 1
C. m ≤ 1
D. m ≤ - 1
Tìm tất cả các giá trị của tham số m để tập xác định của hàm số
y = m x - 2 - x + 1 là một đoạn trên trục số.
A. m<-2
B. m>-2
C. m>2
D. m<2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
x
x
−
m
+
2
−
1
xác định trên (0;1). A.
m
∈
(
−
∞
;
3
2
]
∪
{
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x x − m + 2 − 1 xác định trên (0;1).
A. m ∈ ( − ∞ ; 3 2 ] ∪ { 2 }
B. m ∈ ( − ∞ ; - 1 ] ∪ { 2 }
C. m ∈ ( − ∞ ; 1 ] ∪ { 3 }
D. m ∈ ( − ∞ ; 1 ] ∪ { 2 }
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]