Chọn B.
Phương pháp:
Sử dụng công thức khai triển của nhị thức:
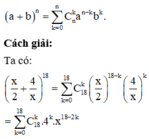
Số hạng không chứa x trong khai triển là số hạng thứ k với: 18 - 2k = 0
=> k = 9
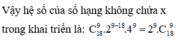
Chọn B.
Phương pháp:
Sử dụng công thức khai triển của nhị thức:
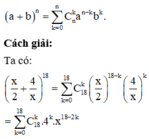
Số hạng không chứa x trong khai triển là số hạng thứ k với: 18 - 2k = 0
=> k = 9
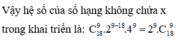
Tìm x
a) 3/4x+ 5/4 =1/4. B)x-3/7=4/8
Tìm 9/15 của số bằng 0,25
6)a) 3/4+-7/9+0.15+1/4+-2/9
b)7/8.-3/6+-3/6.1/8
e)4/6.15.6/4.4
Tìm BcNN và ưcln của 16;32;5
Quy đồng a)-3/8;9/5;-16/32
B) 9/7;24/36;-18/45.
Tìm các dãy tỉ số bằng nhau:
a) \(\frac{x}{4}=\frac{y}{3}=\frac{3}{9}\)và x-3y+4z=62
b) \(\frac{x}{y}=\frac{7}{20};\frac{y}{z}=\frac{5}{8}\)và 2x+5y-2z=100
c) \(\frac{x}{y}=\frac{9}{7};\frac{y}{z}=\frac{7}{3}\)và x-y+z=(-15)
d) \(\frac{6}{11}x=\frac{9}{2}y=\frac{18}{5}z\) và -x+y+z=(-120)
Cho n là số nguyên dương thỏa mãn A n + 3 3 - 6 C n + 1 3 = 294
Tìm số hạng mà tích số mũ của x và y bằng 18 trong khai triển nhị thức Newton: 6 n . x 4 3 y + y 2 x 2 n (với x ≠ 0 ; y ≠ 0 ).
A. 160 x 9 y 2
B. 160 x 2 y 9
C. 160 x 3 y 6
D. 160 x 6 y 3
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tìm hệ số của số hạng chứa x5 trong khai triển (3x-2)8
![]()
![]()
![]()
![]()
Tìm hệ số của x5 trong khai triển P(x)=(1+x)+2(1+x)2+ … + 8(1+x)8
A. 630
B. 635
C. 636
D. 637
a, Tìm x thuộc Z để 2x2+x-18 chia hết cho x-3
b, Tìm các số tự nhiên x,y sao cho 25-y2= 8 (x-2013)2
d) \(\frac{7}{18}\) . x - \(\frac{2}{3}\) = \(\frac{5}{18}\);
e) \(\frac{4}{9}\) - \(\frac{7}{8}\) . x = \(\frac{-2}{3}\);
f) \(\frac{1}{6}\) + \(\frac{-5}{7}\) : x = \(\frac{-7}{18}\)
Tìm hệ số của số hạng không chứa x trong khai triển x − 1 x n . Biết có đẳng thức là:
C n 2 C n n- 2 + 2 C n 2 C n 3 + C n 3 C n n − 3 = 100
A. 9
B. 8
C. 6
D. 7