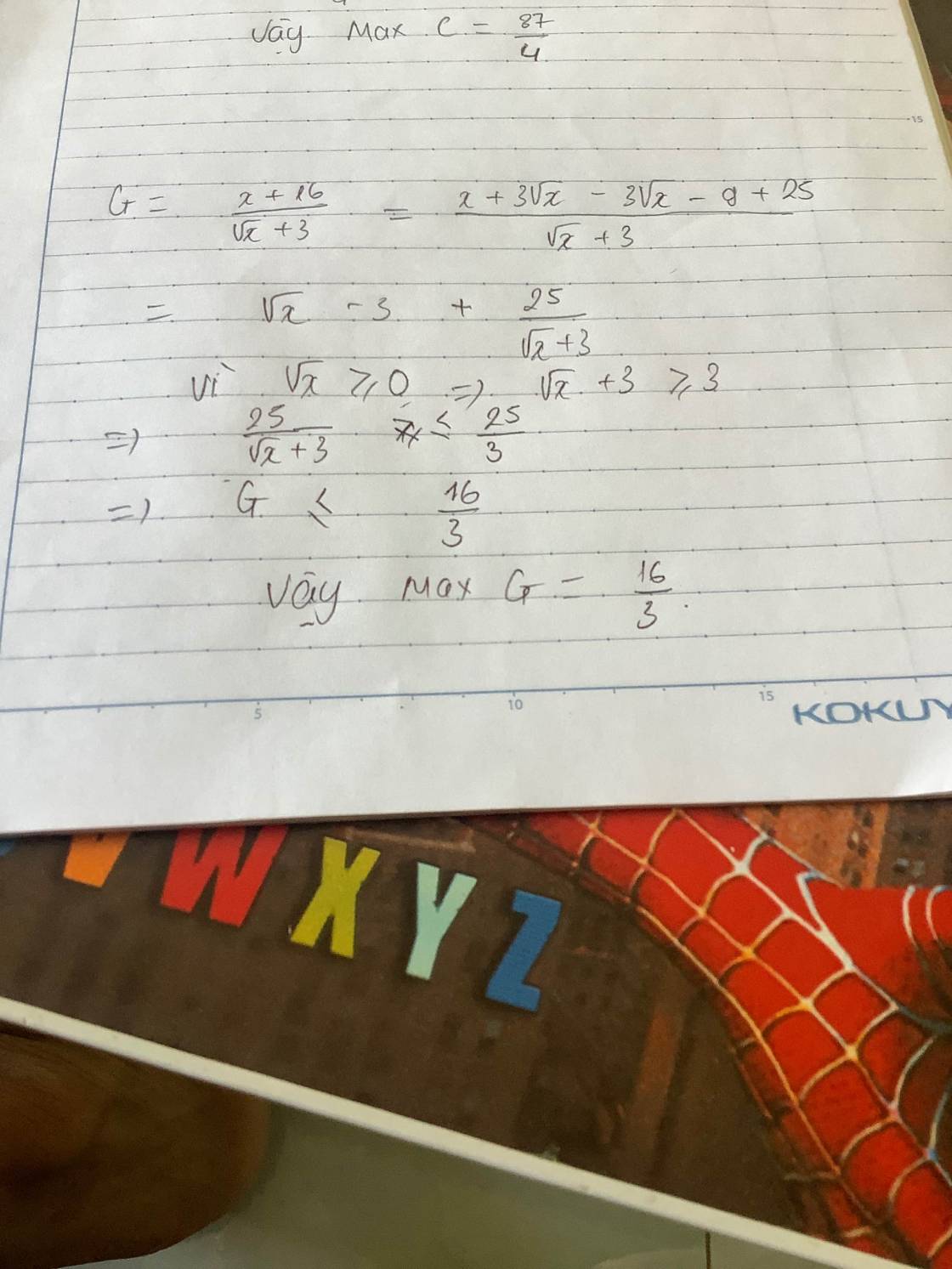\(G=\dfrac{x+16}{\sqrt{x}+3}=\dfrac{\left(x-9\right)+25}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{25}{\sqrt{x}+3}=\left[\left(\sqrt{x}+3\right)+\dfrac{25}{\sqrt{x}+3}\right]-6\)
Áp dụng bất đẳng thức Cô-si, ta có:
\(\left(\sqrt{x}+3\right)+\dfrac{25}{\sqrt{x}+3}\ge2\sqrt{\left(\sqrt{x}+3\right).\dfrac{25}{\sqrt{x}+3}}=2\sqrt{25}=2.5=10\)
\(\Rightarrow G\ge10-6=4\)
Đẳng thức xảy ra \(\Leftrightarrow\left(\sqrt{x}+3\right)^2=25\Leftrightarrow\sqrt{x}+3=5\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\)
Vậy \(MinG=4\Leftrightarrow x=4\)