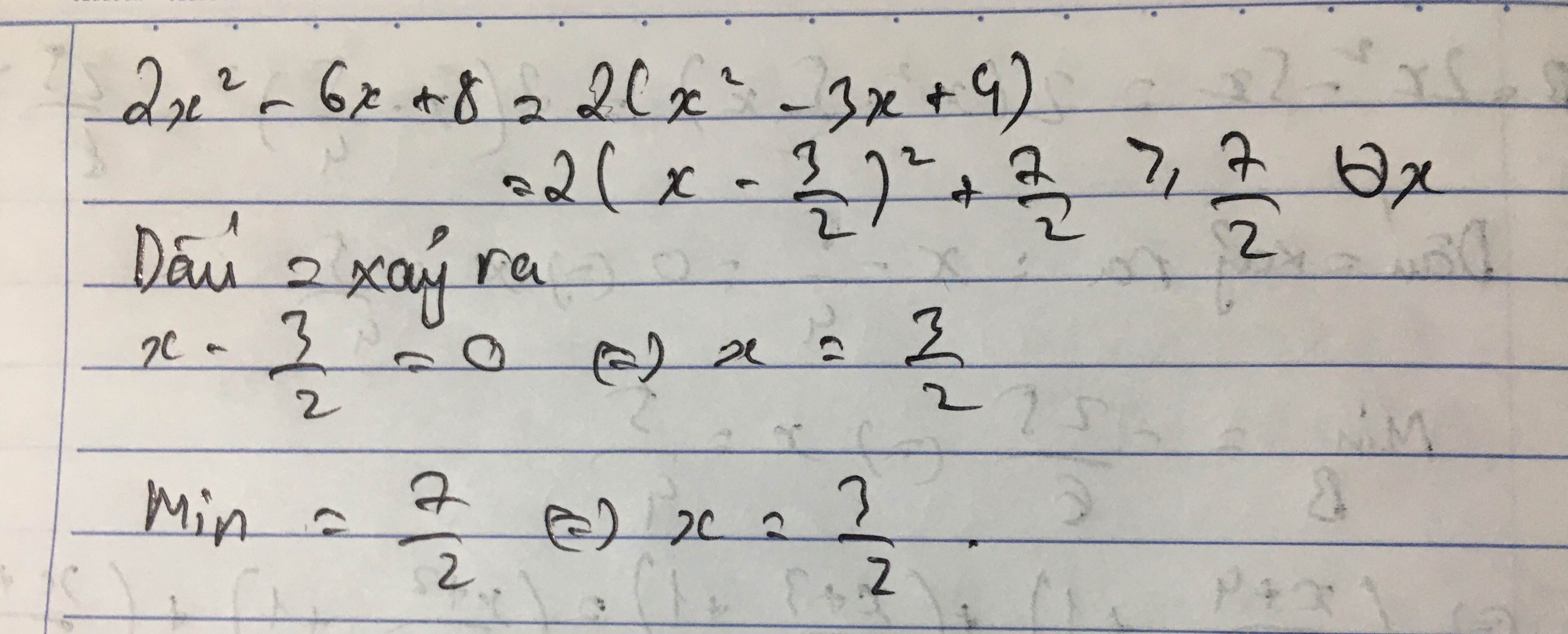\(2x^2-6x+8=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}+8=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{2}\)
Vì \(2\left(x-\dfrac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)
\(ĐTXR\Leftrightarrow x=\dfrac{3}{2}\)
Vậy GTNN của \(2x^2-6x+8\) là \(\dfrac{7}{2}\) khi và chỉ khi \(x=\dfrac{3}{2}\)
Ta có: \(2x^2-6x+8\)
\(=2\left(x^2-3x+4\right)\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\right)\)
\(=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)