Đặt \(A=-3x^2-5y^2+2x+7y-23\)
\(=-3\left(x^2-\dfrac{2}{3}x\right)-5\left(y^2-\dfrac{7}{5}y\right)-23\)
\(=-3\left(x^2-2.\dfrac{1}{3}x+\dfrac{1}{9}-\dfrac{1}{9}\right)-5\left(y^2-2.\dfrac{7}{10}y+\dfrac{49}{100}-\dfrac{49}{100}\right)-23\)
\(=-3\left(x^2-2.\dfrac{1}{3}x+\dfrac{1}{9}\right)+\dfrac{1}{3}-5\left(y^2-2.\dfrac{7}{10}y+\dfrac{49}{100}\right)+\dfrac{49}{20}-23\)
\(=-3\left(x-\dfrac{1}{3}\right)^2-5\left(y-\dfrac{7}{10}\right)^2-\dfrac{1213}{60}\le-\dfrac{1213}{60}\)
Vậy \(A_{max}=-\dfrac{1213}{60}\) khi \(x=\dfrac{1}{3};y=\dfrac{7}{10}\)

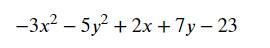




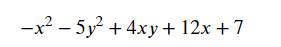
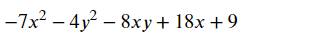 Tìm GTLN của biểu thức sau
Tìm GTLN của biểu thức sau






