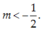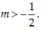\(y=\sqrt{x^2-\left(2m+1\right)x+m-2}\)
\(f\left(x\right)=x^2-\left(2m+1\right)x+m-2\ge0\) đúng với \(x\in\left[-1;2\right]\)
\(TH1:\Delta\le0\Leftrightarrow\left(2m+1\right)^2-4\left(m-2\right)\le0\Leftrightarrow4m^2+9\le0\)(loại)
\(TH2:\)\(\Delta'>0\Leftrightarrow\)\(4m^2+9>0\)(luôn đúng)
\(\Leftrightarrow\left[{}\begin{matrix}2\le x1< x2\left(1\right)\\x1< x2\le-1\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}1f\left(2\right)\ge0\\\dfrac{S}{2}>2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2^2-\left(2m+1\right).2+m-2\ge0\\2m+1>4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le0\\m>\dfrac{3}{2}\end{matrix}\right.\)(loại)
\(\left(2\right)\)\(\Leftrightarrow\left\{{}\begin{matrix}1f\left(-1\right)\ge0\\\dfrac{S}{2}< -1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}1-\left(2m+1\right)\left(-1\right)+m-2\ge0\\2m+1< -2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m< -\dfrac{3}{2}\end{matrix}\right.\)(vô lí) vậy ko có giá trị nào của m thỏa