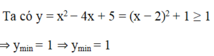Các câu hỏi tương tự
Cho hàm số y 2x^2 - 4mx + 5. Tìm giá trị m để hàm số đạt min 5. Tìm giá trị của m để đường thẳng y 5 cắt đồ thị hàm số y 2x^2 - 4mx + 5 tại 2 điểm phân biệt A và B sao cho AB √6
Cho hàm số y2x^2-4mx+5
a) Tìm giá trị m để hàm số đạt min5
b) Tìm giá trị của m để đường thẳng y5 cắt đồ thị hàm số y2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB căn 6
Đọc tiếp
Cho hàm số y = 2x^2 - 4mx + 5. Tìm giá trị m để hàm số đạt min = 5. Tìm giá trị của m để đường thẳng y = 5 cắt đồ thị hàm số y = 2x^2 - 4mx + 5 tại 2 điểm phân biệt A và B sao cho AB = √6
Cho hàm số y=2x^2-4mx+5
a) Tìm giá trị m để hàm số đạt min=5
b) Tìm giá trị của m để đường thẳng y=5 cắt đồ thị hàm số y=2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB= căn 6
a) Tìm giá trị m để hàm số đạt min=5
b) Tìm giá trị của m để đường thẳng y=5 cắt đồ thị hàm số y=2x^2-4mx+5 tại 2 điểm phân biệt A và B sao cho AB= căn 6
Cho hàm số y = |\(x^2+4x+2m-1\) | với \(\forall x\in\left[-1;3\right]\) . Tìm m để min của y = 5
Tìm min của hàm số : y=giá trị tuyệt đối của (x+1) + căn của (x^2-2x+5)
cho x,y>0 thỏa mãn x+y=7/2. tìm min P= (13x)/3+ 1/2x+ (10y)/3 +9/y
+) Tìm min
\(E=\dfrac{1+\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{z}}{xy+yz+zx}\)
+) Tìm max và min
\(F=\dfrac{a-b}{c}+\dfrac{b-c}{a}+\dfrac{c-a}{b}\)
Trong đó a,b,c>0 và \(min\left\{a,b,c\right\}\ge\dfrac{1}{4}max\left\{a,b,c\right\}\)
Cho \(x-y=\sqrt{3}\)
giá trị nhỏ nhất của biểu thức P = |x - 6| + |y + 1| có dạng \(P_{min}=a\sqrt{3}+b.\), trong đó a,b là số nguyên. Tính giá trị của biểu thức
S = a + b
Cho hai số thực x y, thỏa mãn \(x^2+y^2-2x-4y-4=0\)
cm: \(-2\le x\le4\left(\forall y\in R\right)\)
tìm Min \(S=3x+4y\)
Cho \(x-y=\sqrt{2}\) ,
giá trị nhỏ nhất của Biểu thức P = |2x + 1 | + |2y + 4| có dạng \(P_{min}=a+b\sqrt{2}\), trong đó a,b là số nguyên. tính giá trị của Biểu thức S = a + b
Min F = (x+y)/5 + 4/xy Biết x,y > 0 và (x+y)² ≥ 5(x+y) + 4
cho x,y,z>0 và x+y+z=3 Tìm Min của : \(P=\frac{x+y}{\sqrt{x^2+y^2+6z}}+\frac{y+z}{\sqrt{y^2+z^2+6x}}+\frac{z+x}{\sqrt{z^2+x^2+6y}}\)