Các câu hỏi tương tự
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
z
+
i
z
, với z là số phức khác 0 thỏa mãn
z
≥
2
. Tính 2M-m A. 2M-m
3
2
B. 2M-m
5
2
C. 2M-m 10 D. 2M-m 6
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z + i z , với z là số phức khác 0 thỏa mãn z ≥ 2 . Tính 2M-m
A. 2M-m = 3 2
B. 2M-m = 5 2
C. 2M-m = 10
D. 2M-m = 6
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P
z
+
i
z
, với z là số phức khác 0 và thỏa mãn |z|
≥
2. Tính 2M - m. A. 2M - m
3
2
B. 2M - m
5
2
C. 2M - m 10 D. 2M - m 6
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z + i z , với z là số phức khác 0 và thỏa mãn |z| ≥ 2. Tính 2M - m.
A. 2M - m = 3 2
B. 2M - m = 5 2
C. 2M - m = 10
D. 2M - m = 6
Trong không gian Oxyz, cho đường thẳng
d
:
x
-
2
3
y
+
1
1
z
+
5
-
1
và mặt phẳng (P):2x-3y+z-60. Phương trình nào...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x - 2 3 = y + 1 1 = z + 5 - 1 và mặt phẳng (P):2x-3y+z-6=0. Phương trình nào dưới đây là phương trình của đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với (d)?
![]()
![]()
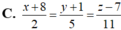
![]()
Cho số phức z thỏa mãn
z
.
z
2
và
z
-
2
-
1
-
z
là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
Đọc tiếp
Cho số phức z thỏa mãn z . z = 2 và z - 2 - 1 - z là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
![]()
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.
z
¯
1 và |z -
3
+ i|. Tìm số phần tử của S A. 1. B. 2. C. 3. D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của
P
z
+
i
z
, với z là số phức khác 0 và thỏa mãn
z
≥
2
. Tính tỷ số
M
m
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của P = z + i z , với z là số phức khác 0 và thỏa mãn z ≥ 2 . Tính tỷ số M m
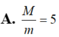
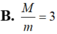
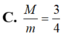
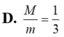
Cho số phức z thỏa mãn z ≥ 2 . Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức P = z + i z
A. 3 4
B. 1
C. 2
D. 2 3
Cho số phức z thỏa điều kiện
z
+
2
z
+
2
i
. Giá trị nhỏ nhất của biểu thức
P
z
-
1
-
2...
Đọc tiếp
Cho số phức z thỏa điều kiện z + 2 = z + 2 i . Giá trị nhỏ nhất của biểu thức P = z - 1 - 2 i + z - 3 - 4 i + z - 5 - 6 i được viết dưới dạng a + b 17 2 với a, b là các hữu tỉ. Giá trị của a + b là
A. 4.
B. 2.
C. 7.
D. 3.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
3
2
y
+
2
1
z
+
1
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 2 = y + 2 1 = z + 1 - 1 và mặt phẳng (P):x+y+z+2=0. Đường thẳng ∆ nằm trong mặt phẳng (P) vuông góc với đường thẳng d đồng thời khoảng cách từ giao điểm I của d với (P) đến ∆ bằng 42 . Gọi M(5;b;c) là hình chiếu vuông góc của I trên ∆ . Giá trị của bc bằng
A. -10
B. 10
C. 12
D. -20


