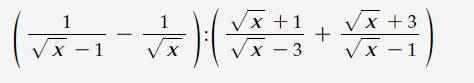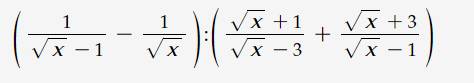Lời giải:
ĐKXĐ: $x>0; x\neq 1; x\neq 9$
\(A=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{(\sqrt{x}+1)(\sqrt{x}-1)+(\sqrt{x}+3)(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}-1)}\)
\(=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{x-1-(x-9)}{(\sqrt{x}-3)(\sqrt{x}-1)}=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{8}{(\sqrt{x}-1)(\sqrt{x}-3)}\)
\(=\frac{1}{\sqrt{x}(\sqrt{x}-1)}.\frac{(\sqrt{x}-1)(\sqrt{x}-3)}{8}=\frac{\sqrt{x}-3}{8\sqrt{x}}\)
Để $A<0\Leftrightarrow \frac{\sqrt{x}-3}{8\sqrt{x}}<0$
$\Leftrightarrow \sqrt{x}-3<0$ (do $8\sqrt{x}>0$)
$\Leftrightarrow \sqrt{x}<3$
$\Leftrightarrow 0\leq x< 9$
Kết hợp với đkxđ suy ra $0< x< 9; x\neq 1$
Khi $x=3-2\sqrt{2}=(\sqrt{2}-1)^2$
$\Rightarrow \sqrt{x}=\sqrt{2}-1$
Khi đó: $A=\frac{\sqrt{x}-3}{8\sqrt{x}}=\frac{\sqrt{2}-4}{8(\sqrt{2}-1)}=\frac{-2-3\sqrt{2}}{8}$