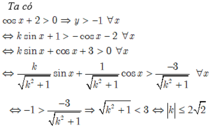Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Tìm k để GTNN của hàm số
y
k
sin
x
+
1
cos
x
+
2
lớn hơn -1? A.
|
k
|
≤
2
B.
|
k
|
≤
2
3
C. ...
Đọc tiếp
Tìm k để GTNN của hàm số y = k sin x + 1 cos x + 2 lớn hơn -1?
A. | k | ≤ 2
B. | k | ≤ 2 3
C. | k | ≤ 2 2
D. | k | ≤ 3
Tìm k để giá trị nhỏ nhất của hàm số
y
ksinx
+
1
cosx
+
2
lớn hơn -1. A.
k
2
B.
k
2
3
C. ...
Đọc tiếp
Tìm k để giá trị nhỏ nhất của hàm số y = ksinx + 1 cosx + 2 lớn hơn -1.
A. k < 2
B. k < 2 3
C. k < 3
D. k < 2 2
Cho đa thức K (x) = a+b (x - 1) + c (x - 1). (x - 2)
Tìm a; b; c biết K (1) = 1, K (2) =2; K (0) = 5
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−
16
9...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−
16
9...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
bài 1)cho x^2+y^2=52
tìm GTLN của H=2x+3y
bài 2) cho x>0;y>0; x+y=1
tìm GTNN của K=1/x^2+y^2 + 1/xy
Đường thẳng x k cắt đồ thị hàm số
y
log
5
x
và đồ thị hàm số
y
log
3
(
x
+
4
)
. Khoảng cách giữa các giao điểm là 1/2. Biết
k
a
+
b
,
trong đó a, b là các số nguyên. Khi đó tổng a + b bằng A. 7 B. 6 C. 8 D. 5
Đọc tiếp
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
1. Cho p và p2 - 1 là số nguyên tố ( p > 3 ) . Chứng minh 8p2+1 là hợp số
2.a. Nếu p và q là 2 số nguyên tố lớn hơn 3 thì p2-q2 chia hết cho 24
b. Nếu a, a+ k , a + 2k ( a, k khác 0 ) là các số nguyên tố lớn hơn 3 thì k chia hết cho 6