Các câu hỏi tương tự
Hàm số nào sau đây không có cực trị
A: \(y=\dfrac{x^2+1}{x}\)
B: \(y=\dfrac{2x-x}{x+1}\)
C: \(y=x^2-2x+1\)
D: \(y=-x^3+x+1\)
Cho hàm số f(x) có đạo hàm f'(x) = \(x\left(1-x\right)^2\left(3-x\right)^3\left(x-2\right)^4\) . Điểm cực tiểu của hàm số đã cho là
A: x = 2
B: x = 3
C: x = 0
D: x = 1
Ai có bảng biến thiên thì vẽ cho dễ hiểu
Giá trị nhỏ nhất của hàm số \(y=\sqrt{4-x}+\sqrt{3}\) trên tập xác định của nó là
A: 2 + \(\sqrt{3}\)
B: 2\(\sqrt{3}\)
C: 0
D: \(\sqrt{3}\)
Tập xác định D của hàm số
y
(
x
2
-
3
x
+
2
)
3
5
+
(
x
-
3
)
-
2
là
Đọc tiếp
Tập xác định D của hàm số
y = ( x 2 - 3 x + 2 ) 3 5 + ( x - 3 ) - 2 là
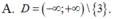
![]()
![]()
![]()
Đạo hàm của hàm số
y
-
x
2
+
3
x
-
3
2
(
x
-
1
)...
Đọc tiếp
Đạo hàm của hàm số y = - x 2 + 3 x - 3 2 ( x - 1 ) bằng biểu thức có dạng ax 2 + bx 2 ( x - 1 ) 2 . Khi đó a.b bằng
A. -1 .
B. 6 .
C. 4 .
D. -2 .
Tập xác định của hàm số y
x
2
-
3
x
+
2
3
5
+
x
-
3
-
2
là
A...
Đọc tiếp
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A . D = ( - ∞ ; + ∞ ) \ { 3 }
B . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C . D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Tập xác định của hàm số
y
x
2
-
3
x
+
2
3
5
+
x
-
3
-
2
là A. D
(...
Đọc tiếp
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A. D= ( - ∞ ; + ∞ ) \ { 3 }
B. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C. D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Tìm m để đồ thị hàm số
y
x
3
+
3
x
2
+
m
x
+
2
m
cắt đường thẳng y -x + 2 tại 3 điểm. A.
m
5
4
B. m 1 C.
m
5
4
và
m
≠
-
1
D.
-
1
m
5...
Đọc tiếp
Tìm m để đồ thị hàm số y = x 3 + 3 x 2 + m x + 2 m cắt đường thẳng y = -x + 2 tại 3 điểm.
A. m > 5 4
B. m > 1
C. m < 5 4 và m ≠ - 1
D. - 1 < m < 5 4
Hàm số \(y=-x^3+3x^2-4\) đồng biến trên tập hợp nào sau đây:
A:(2;+∞)
B:(0;2)
C:(-∞;0)\(\cup\) (2;+∞)
D:(-∞;0)