\(y'=-3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Hàm đồng biến trên \(\left(0;2\right)\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Tìm các khoảng đồng biến của hàm số: y = 2sinx + cos2x, x ∈ [0;π] A. (0; pi/2 B. (pi/2; pi) C. (0; pi/6) và pi/2; 5pi/6) D. (0;pi).
Hàm số nào trong các hàm số sau đây đồng biến trên R A.
y
x
2
-
2
x
+
3
B.
y
x
3
+
x
C.
y
1
+
1
(
x
2...
Đọc tiếp
Hàm số nào trong các hàm số sau đây đồng biến trên R
A. y = x 2 - 2 x + 3
B. y = x 3 + x
C. y = 1 + 1 ( x 2 + 1 )
D. y = l n ( x 2 + 1 )
Giá trị nhỏ nhất của hàm số \(y=\sqrt{4-x}+\sqrt{3}\) trên tập xác định của nó là
A: 2 + \(\sqrt{3}\)
B: 2\(\sqrt{3}\)
C: 0
D: \(\sqrt{3}\)
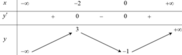
Cho hàm số yf(x) có bảng biến thiên như hình.Hàm số đã cho đồng biến trên khoảng A.
-
∞
;
-
1
B. (-1;3) C. (-3;0) D.
(
0
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình.
Hàm số đã cho đồng biến trên khoảng
A. - ∞ ; - 1
B. (-1;3)
C. (-3;0)
D. ( 0 ; + ∞ )
Cho hàm số yf(x) có bảng biến thiên như hìnhHàm số đã cho đồng biến trên khoảng A.
-
∞
;
-
1
B.
-
1
;
3
C.
-
3
;
0
D. ...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình
Hàm số đã cho đồng biến trên khoảng
A. - ∞ ; - 1
B. - 1 ; 3
C. - 3 ; 0
D. 0 ; + ∞
Cho hàm số y = x 3 - 6 x 2 + 9 x + 7 . Hàm số đồng biến trên khoảng
A. (1; 3)
B. (1; +∞)
C. (-∞; 3)
D. (-∞; 1) và (3; +∞)
Tập xác định D của hàm số
y
(
x
2
-
3
x
+
2
)
3
5
+
(
x
-
3
)
-
2
là
Đọc tiếp
Tập xác định D của hàm số
y = ( x 2 - 3 x + 2 ) 3 5 + ( x - 3 ) - 2 là
Tìm khoảng đồng biến của hàm số
y
-
x
3
+
3
x
2
-
2
Đọc tiếp
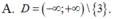
Tìm khoảng đồng biến của hàm số y = - x 3 + 3 x 2 - 2
Cho hàm số f(x) có đạo hàm f'(x) = \(x\left(1-x\right)^2\left(3-x\right)^3\left(x-2\right)^4\) . Điểm cực tiểu của hàm số đã cho là
A: x = 2
B: x = 3
C: x = 0
D: x = 1
Ai có bảng biến thiên thì vẽ cho dễ hiểu