Tập xác định R.
Ta có:
y ' = 2 x e - 4 x + x 2 e - 4 x ( - 4 ) = 2 e - 4 x x ( 1 - 2 x )
Bảng biến thiên
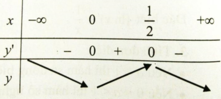
Khoảng đồng biến của hàm số là (0; 1/2) .
Chọn đáp án C
Tập xác định R.
Ta có:
y ' = 2 x e - 4 x + x 2 e - 4 x ( - 4 ) = 2 e - 4 x x ( 1 - 2 x )
Bảng biến thiên

Khoảng đồng biến của hàm số là (0; 1/2) .
Chọn đáp án C
cho y=1/3x³-(m-2)x²+(m²-3m+2)x+3. tìm m để a)Hàm số đồng biến với mọi x thuộc (2;dương vô cùng) b)Hàm số đồng biến với mọi x thuộc (trừ âm vô cùng;0) c)Hàm số nghịch biến với mọi x thuộc (-2;3)
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Hàm số y = - x 4 2 + 1 đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).
Tìm a ∈ (0; 2 π ) để hàm số sau đồng biến trên khoảng (1; + ∞ ).
y = 1 3 x 3 - 1 2 (1 + cosa) x 2 + 2x cosa + 1
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
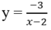
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
y = - 3 x - 2
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3
tìm m để hàm số y = -x^3 + 3mx^2 - 2 luôn nghịc biến R
A. m = 0.
B. m > 0.
C. m ≠ 0.
D. M < 0.
Chứng minh rằng hàm số y = 2 x - x 2 đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Hàm số 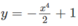 đồng biến trên khoảng:
đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).