Đáp án: A.
Hàm số dạng này có một điểm cực đại tại x = 0. Vậy hàm số đồng biến trên khoảng (- ∞ ; 0).
Đáp án: A.
Hàm số dạng này có một điểm cực đại tại x = 0. Vậy hàm số đồng biến trên khoảng (- ∞ ; 0).
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Hàm số 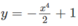 đồng biến trên khoảng:
đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).
Cho hàm số y = x − 2 x − 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên − ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ 1 .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞ .
Số mệnh đề đúng là
A. 3
B. 2
C. 1
D. 4
Cho bốn hàm số sau : y= f(x) = lnx ; y = g ( x ) = 2 x 2 + 4 ; y = h ( x ) = 2017 1018 x và
y= l(x)= ln( x2+1). Có bao nhiêu hàm số đồng biến trên khoảng ( 0 ; + ∞ )
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = x + 1 1 - x và các mệnh đề sau
(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,
(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.
(3) Hàm số trên nhận y = -1 là tiệm cận đứng.
(4) Hàm số trên luôn đồng biến trên R.
Trong số các mệnh đề trên, số mệnh đề sai là
A. 1
B. 2
C. 3
D. 4
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định
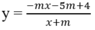
A. m < 1 hoặc m > 4 B. 0 < m < 1
C. m > 4 D. 1 ≤ m ≤ 4
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Tìm giá trị của tham số m để các hàm số y = x 3 - 2m x 2 + 12x - 7 đồng biến trên R.
A. m = 4 B. m ∈ (0; ∞ )
C. m ∈ (- ∞ ; 0) D. -3 ≤ m ≤ 3