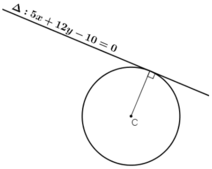
Vì đường tròn tâm C tiếp xúc với Δ nên R = d(C, Δ).
Do đó ta có :
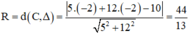

Vì đường tròn tâm C tiếp xúc với Δ nên R = d(C, Δ).
Do đó ta có :
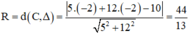
Tính bán kính của đường tròn tâm A (2; -1) tiếp xúc với đường thẳng \(\Delta:-2x+10y-7=0\)
Nếu đường tròn (C): (x-1)2+ (y-3) 2 = R2 tiếp xúc với đường thẳng d: 5x+ 12y – 60 =0 thì giá trị của R là:
A. R= 1
B. R= 19 13
C. R= 2
D. R= 2/3
Cho đường tròn (C) có tâm I(2; 5) và tiếp xúc với đường thẳng ∆: 3x – 4y – 6 = 0. Khi đó (C) có bán kính là:
A.R = 2
B. R = 2 2
C. R = 3
D.R = 4
Bán kính đường tròn (C) có tâm I(-1;2) và tiếp xúc với đường thẳng d: x + 2y + 7 = 0 bằng:
A. R = 5
B. R = 2 5
C. R = 1 5
D. R = 2
Đường tròn (C) đi qua hai điểm A(1; 2); B(3;4) và tiếp xúc với đường thẳng Δ : 3 x + y − 3 = 0 . Viết phương trình đường tròn (C), biết tâm của (C) có tọa độ là những số nguyên.
A. x 2 + y 2 − 3 x – 7 y + 12 = 0.
B. x 2 + y 2 − 6 x – 4 y + 5 = 0.
C. x 2 + y 2 − 8 x – 2 y − 10 = 0.
D. x 2 + y 2 − 2 x − 8 y + 20 = 0.
Đường tròn có tâm nằm trên đường thẳng ∆: x + 2y – 6 = 0 và tiếp xúc với hai trục tọa độ. Khi đó bán kính của đường tròn là
A.R = 2 hoặc R = 4
B.R = 2 hoặc R = 6
C.R = 3 hoặc R = 6
D.R = 3 hoặc R = 4
Cho đường tròn (C) có tâm nằm trên đường thẳng ∆: x + 2y – 5 = 0 và tiếp xúc với hai đường thẳng d 1 : 3 x − y + 5 = 0 v à d 2 : x + 3 y − 13 = 0 . Khi đó bán kính lớn nhất của đường tròn (C) có thể nhận là:
A. 19 2 10
B. 3 10
C. 9 2 10
D. 6 10
Lập phương trình đường tròn có tâm nằm trên đường thẳng Δ: 4x + 3y – 2 = 0 và tiếp xúc với hai đường thẳng d1: x + y + 4 = 0 và d2: 7x – y + 4 = 0 .
Cho điểm A(7; 4) và đường thẳng ∆: 3x – 4y + 8 = 0. Bán kính đường tròn tâm A và tiếp xúc với ∆ là:
A.13/5
B.3/5
C.7/5
D.3/2