Đường tròn : C): (x-1)2+ (y-3) 2 = R2 có tâm I( 1;3) bán kính R.
Để đường thẳng d tiếp xúc với đường tròn (C) khi
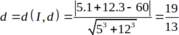
Chọn B.
Đường tròn : C): (x-1)2+ (y-3) 2 = R2 có tâm I( 1;3) bán kính R.
Để đường thẳng d tiếp xúc với đường tròn (C) khi
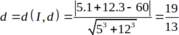
Chọn B.
Đường tròn C có tâm I (3,-2) và bán kính R=3 . Viết phương trình tiếp tuyến vuông góc với đường thẳng ∆:=x-y-1=0
Trong mặt phẳng Oxy, (C) tâm I bán kính R = 2. Lấy M trên đường thẳng d: x+y=0. Từ M kẻ 2 tiếp tuyến MA,MB đến (C) ( A, B là tiếp điểm). Biết phương trình đường thẳng AB: 3x+y-2=0 và khoảng cách từ tâm I đến d = 2 căn 2 . Viết ptrinh đường tròn (C)
Trong các tập hợp sau, tập nào là tập con của tập nào?
a)A={1;2}, B={x∈N|x≤3},
C=[1;+∞), D={x∈R|2x2-5x+2=0}
b)A={1;3}, B={x∈Z|-1≤x≤2},
C=(0;+∞), D={x∈R|(x-1)(2-x)(x-3)=0}
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Tìm tọa độ giao điểm của đường thẳng (d): \(\left\{{}\begin{matrix}x=2+t\\y=-1+3t\end{matrix}\right.\) (t ∈ R) với đường tròn (C):x2+y2-2x-1=0
Câu 1: Cho 2 điểm A,B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|2.vectoMA+vectoMB\right|=\left|vectoMA+2.vectoMB\right|\)là:
A. đường trung trực của đoạn AB
B. đường tròn đường kính AB
C. đường trung trực đoạn thẳng IA
D. đường tròn tâm A, bán kính AB
Câu 2: cho tam giác ABC đều cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức \(\left|3.vectoMA+3.vectoMB+4.vectoMC\right|=\left|vectoMB-vectoMA\right|\)là đường tròn cố định có bán kính R. Tính bán kính R theo a.
A. R = a/3
B. R = a/9
C. R = a/2
D. R = a/6
Câu 3: Cho hình chữ nhật ABCD và số thực K>0. Tập hợp các điểm M thỏa mãn đẳng thức \(\left|vectoMA+vectoMB+vectoMC+vectoMD\right|=k\)là:
A. một đoạn thẳng
B. một đường thẳng
C. một đường tròn
D. một điểm
Câu 4:Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn \(\left|vectoMA+vectoMB+vectoMC\right|=3\)?
A.1
B.2
C.3
D. vô số
Đường tròn x^2+y^2-4x-6y=12 có tâm I và bán kính R. Với O là gốc tọa độ, mệnh đề nào đúng?
A.OI>R
B. OI=R
C.5OI=R4,123
D.5OI=R3,742
Tìm bán kính của đường tròn tâm C(-2; -2) tiếp xúc với đường thẳng Δ : 5x + 12y -10 = 0.
Viết phương trình đường tròn Tâm I tiếp xúc với đường thẳng d: 3x-4y-31=0 tại điểm M(1:7) và bán kính R=5