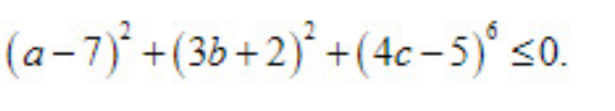Vì `(a-7)^{2}>=0` với mọi `a`
`(3b+2)^{2}>=0` với mọi `b`
`(4c-5)^{2}>=0` với mọi `c`
`->(a-7)^{2}+(3b+2)^{2}+(4c-5)^{2}>=0` với mọi `a;b;c`
Mà để : `(a-7)^{2}+(3b+2)^{2}+(4c-5)^{2}\le0`
`->(a-7)^{2}+(3b+2)^{2}+(4c-5)^{2}=0`
`->a-7=0` và `3b+2=0` và `4c-5=0`
`->a=7` và `b=-2/3` và `x=5/4`
Ta có: \(\left(a-7\right)^2\ge0\forall a\)
\(\left(3b+2\right)^2\ge0\forall b\)
\(\left(4c-5\right)^6\ge0\forall c\)
Do đó: \(\left(a-7\right)^2+\left(3b+2\right)^2+\left(4c-5\right)^6\ge0\forall a,b,c\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a=7\\b=-\dfrac{2}{3}\\c=\dfrac{5}{4}\dfrac{4}{ }\end{matrix}\right.\)