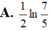Các câu hỏi tương tự
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
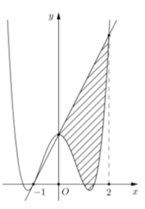
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số y f(x) có đạo hàm f(x)0,
∀
x
∈
1
;
2
thỏa mãn f(1) 1, f(2) 22/14 và
∫
1
2
f
x
3
x
4...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x)>0, ∀ x ∈ 1 ; 2 thỏa mãn f(1) = 1, f(2) = 22/14 và ∫ 1 2 f ' x 3 x 4 d x = 7 375 . Tích phân ∫ 1 2 f x d x bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số yf(x) có đạo hàm trên
ℝ
thỏa mãn
3
f
(
x
)
.
e
f
3
(
x
)
-
x
2
-
1
-
2
x
f...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ thỏa mãn 3 f ' ( x ) . e f 3 ( x ) - x 2 - 1 - 2 x f 2 ( x ) = 0 và f(0)=1 . Tích phân ∫ 0 7 x . f ( x ) d x bằng:
A. 2 7 3
B. 15 4
C. 45 8
D. 5 7 4
Cho hàm số
f
(
x
)
x
+
1
k
h
i
x
≥
0
e...
Đọc tiếp
Cho hàm số f ( x ) = x + 1 k h i x ≥ 0 e 2 x k h i x ≤ 0 . Tích phân I = ∫ - 1 2 f ( x ) d x có giá trị bằng bao nhiêu?
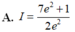
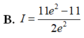
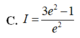
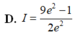
tích phân từ 1 đến 2 f(x)đc= 2 . Giá trị của tích phân từ 1 đến 3f(x)đc bằng
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
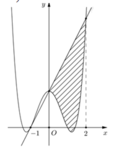
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số y f (x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(0)1;
∫
0
1
(
1
-
x
)
2
f
(
x
)
d
x
1
3
. Giá trị nhỏ nhất của tích phân bằng
∫
0
1
f...
Đọc tiếp
Cho hàm số y = f (x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(0)=1; ∫ 0 1 ( 1 - x ) 2 f ' ( x ) d x = 1 3 . Giá trị nhỏ nhất của tích phân bằng ∫ 0 1 f 2 ( x ) d x bằng
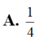
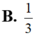
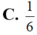
![]()
Một hình phẳng được giới hạn bởi y
e
-
x
, y 0, x 0, x 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên). Tìm
lim
n
→
∞
S
n
và so sánh với...
Đọc tiếp
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên). Tìm lim n → ∞ S n và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.