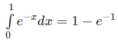Các câu hỏi tương tự
Một hình phẳng được giới hạn bởi y
e
-
x
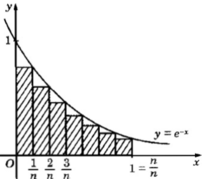
, y 0, x 0, x 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).b) Tìm và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Đọc tiếp
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm 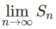 và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Một hình phẳng được giới hạn bởi y
e
-
x
, y 0, x 0, x 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên). Tính diện tích
S
n
của hình bậc thang (tổng diện tích của n hình chữ nhật con).
Đọc tiếp
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên). Tính diện tích S n của hình bậc thang (tổng diện tích của n hình chữ nhật con).
Xét hình phẳng (H) được giới hạn bởi các đường thẳng y0, x0 và đường
y
x
+
3
2
. Gọi
A
0
;
9
,
B
b
;
0
−
3
b...
Đọc tiếp
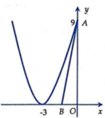
Xét hình phẳng (H) được giới hạn bởi các đường thẳng y=0, x=0 và đường y = x + 3 2 . Gọi A 0 ; 9 , B b ; 0 − 3 < b < 0 . Tìm giá trị của b để đoạn thẳng AB chia (H) thành hai phần có diện tích bằng nhau?
A. b = - 2
B. b = − 1 2
C. b = − 1
D. b = − 3 2
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
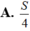
![]()
![]()
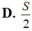
Cho hình phẳng (D) được giới hạn bởi các đường x0, x1, y0 và
y
2
x
+
1
.Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0, x=1, y=0 và y = 2 x + 1 .Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
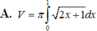
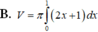
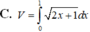
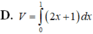
Cho hình phẳng (D) được giới hạn bởi các đường x 0; x 1; y 0 và
y
2
x
+
1
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0; x = 1; y = 0 và y = 2 x + 1 . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
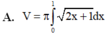
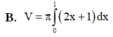
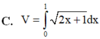
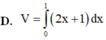
Hình phẳng giới hạn bởi đồ thị hàm số
y
e
x
.
sin
x
và các đường thẳng x 0, x π, trục hoành. Một đường x k cắt diện tích trên tạo thành 2 phần có diện tích bằng
S
1
,
S
2
sao cho
(
2
S
1
+
2
S
2...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y = e x . sin x và các đường thẳng x = 0, x = π, trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 , S 2 sao cho ( 2 S 1 + 2 S 2 - 1 ) = ( 2 S 1 - 1 ) 2 khi đó k bằng:
A. π 4
B. π 2
C. π 3
D. π 6
Cho hình phẳng (D) được giới hạn bởi các đường x0;
x
π
; y 0 và y -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0; x = π ; y = 0 và y = -sinx. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
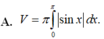
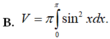
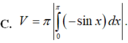
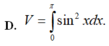
Gọi (D) là hình phẳng giới hạn bởi các đường
y
2
x
,
y
0
,
x
0
v
à
x
2
. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức: A.
V
π
∫
0
2...
Đọc tiếp
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x