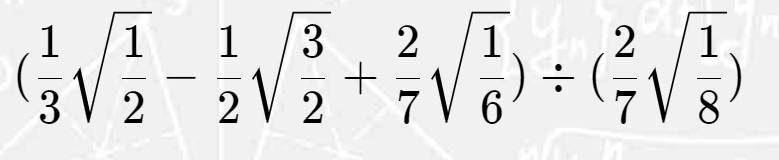\(\left(\dfrac{1}{3}\sqrt{\dfrac{1}{2}}-\dfrac{1}{2}\sqrt{\dfrac{3}{2}}+\dfrac{2}{7}\sqrt{\dfrac{1}{6}}\right):\left(\dfrac{2}{7}\sqrt{\dfrac{1}{8}}\right)\)
\(=\left(\dfrac{1}{3}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{6}}{2}+\dfrac{2}{7}\cdot\dfrac{\sqrt{6}}{6}\right):\left(\dfrac{2}{7}\cdot\sqrt{\dfrac{2}{16}}\right)\)
\(=\left(\dfrac{\sqrt{2}}{6}-\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{6}}{21}\right):\left(\dfrac{2}{7}\cdot\dfrac{\sqrt{2}}{4}\right)\)
\(=\left(\dfrac{14\sqrt{2}-21\sqrt{6}+4\sqrt{6}}{84}\right):\dfrac{2\sqrt{2}}{28}\)
\(=\dfrac{14\sqrt{2}-17\sqrt{6}}{84}\cdot\dfrac{14}{\sqrt{2}}\)
\(=\dfrac{14}{84}\cdot\dfrac{\sqrt{2}\left(14-17\sqrt{3}\right)}{\sqrt{2}}\)
\(=\dfrac{14-17\sqrt{3}}{6}\)