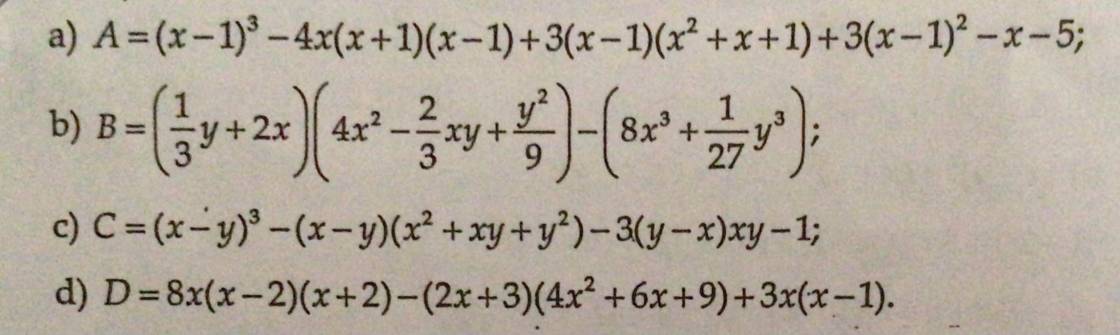\(D=8x\left(x-2\right)\left(x+2\right)-\left(2x+3\right)\left(4x^2+6x+9\right)+3x\left(x-1\right)\\ =8x\left(x^2-4\right)-\left(2x+3\right)\left(2x+3\right)^2+3x\left(x-1\right)\\ =8x^3-32x-\left(2x+3\right)^3+3x^2-3x\\ =8x^3-32x-\left(8x^3+36x^2+54x+27\right)+3x^2-3x\\ =\left(8x^3-8x^3\right)-\left(36x^2-3x^2\right)-\left(32x+54x+3x\right)-27\\ =-33x^2+89x-27\)
\(B=\left(\dfrac{1}{3}y+2x\right)\left(4x^2-\dfrac{2}{3}xy+\dfrac{y^2}{9}\right)-\left(8x^3+\dfrac{1}{27}y^3\right)\\ =\left(\dfrac{1}{3}y+2x\right)\left[\left(2x\right)^2-2x.\dfrac{1}{3}y+\left(\dfrac{1}{3}y\right)^2\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]-\left[\left(2x\right)^3+\left(\dfrac{1}{3}y\right)^3\right]\\ =0\)
\(A=\left(x-1\right)^3-4x\left(x+1\right)\left(x-1\right)+3\left(x-1\right)\left(x^2+x+1\right)+3\left(x-1\right)^2-x-5\\ =\left(x^3-3x^2+3x-1\right)-4x\left(x^2-1\right)+3\left(x^3-1\right)+3\left(x^2-2x+1\right)-x-5\\ =x^3-3x^2+3x-1-4x^3+4x+3x^3-3+3x^2-6x+3-x-5\\ =\left(x^3-4x^3+3x^3\right)+\left(3x^2-3x^2\right)+\left(3x+4x-6x-x\right)-\left(1+3-3+5\right)\\ =0+0+0-6=-6\)