Các câu hỏi tương tự
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD. A.
a
2
3
4
B.
a
2
3
9
C. ...
Đọc tiếp
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC
120
o
,ABACa Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là
V
a
3
16
Đọc tiếp
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC= 120 o ,AB=AC=a Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16

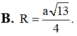
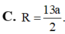
![]()
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
A
.
2
45
B
.
9
34
C
....
Đọc tiếp
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
A . 2 45
B . 9 34
C . 2 5
D . 4 15
Cho tứ diện ABCD. M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Thiết diện của tứ diện với mặt phẳng (∝) chứa MN và song song với AB là hình gì?
A. tam giác
B. hình bình hành
C. hình thoi
D. hình thang có đúng một cặp cạnh song song
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là A.
a
2
3
2
.
B.
a
2
2
4
.
C.
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 3 2 .
B. a 2 2 4 .
C. a 2 2 6 .
D. a 2 4 4 .
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 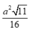
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
0
.Tính theo a thể tích khối tứ diện SABC
A
.
a
3
6
3
B
.
a...
Đọc tiếp
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 0 .Tính theo a thể tích khối tứ diện SABC
A . a 3 6 3
B . a 3 3 3
C . 2 a 3 6 3
D . a 3 2 3
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là
G
1
,
G
2
.Tìm câu đúng nhất.Thiết diện của hình tứ diện cắt bởi mặt phẳng (
B
G
1
G
2
) là: A. Tam giác B. Tứ giác C. Tam giác cân D. Hình thang
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 .
Tìm câu đúng nhất.
Thiết diện của hình tứ diện cắt bởi mặt phẳng ( B G 1 G 2 ) là:
A. Tam giác
B. Tứ giác
C. Tam giác cân
D. Hình thang
Cho khối lăng trụ tam giác ABC.
A
1
B
1
C
1
có đáy là tam giác đều cạnh a,
A
1
A
a
2
và
A
1
A
tạo với mặt phẳng (ABC) một góc
30
o
Tính thể tích khối tứ diện
A...
Đọc tiếp
Cho khối lăng trụ tam giác ABC. A 1 B 1 C 1 có đáy là tam giác đều cạnh a, A 1 A = a 2 và A 1 A tạo với mặt phẳng (ABC) một góc 30 o Tính thể tích khối tứ diện A 1 B 1 C A là
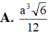
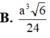
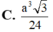
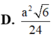
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A
.
a
2
11
2
B
.
a
2
2...
Đọc tiếp
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A . a 2 11 2
B . a 2 2 4
C . a 2 11 4
D . a 2 3 4



