Chọn A.
Gọi r, h, V tương ứng là bán kính đáy, chiều cao và thể tích của khối trụ. Ta dễ dàng thấy r 2 + h 2 4 = R 2
Và từ đó
Bây giờ sử dụng bất đẳng thức Cauchy ta có
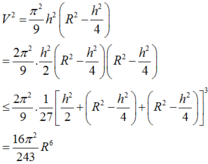
Suy ra V ≤ 4 π 9 3 R 3 . Đẳng thức xảy ra khi và chỉ khi

Chọn A.
Gọi r, h, V tương ứng là bán kính đáy, chiều cao và thể tích của khối trụ. Ta dễ dàng thấy r 2 + h 2 4 = R 2
Và từ đó
Bây giờ sử dụng bất đẳng thức Cauchy ta có
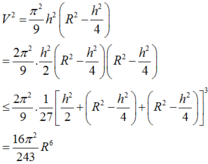
Suy ra V ≤ 4 π 9 3 R 3 . Đẳng thức xảy ra khi và chỉ khi

Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Cho khối cầu (S) có tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
A. R 2
B. R 3 3
C. 4
D. 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
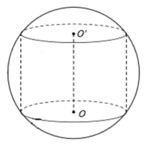
A. h = 2 R 3 3 .
B. h = R 2 2 .
C. h = R 3 3 .
D. h = R 2 .
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất
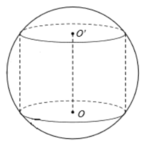
A. h = 2 R 3 3
B. h = R 2 2
C. h = R 3 3
D. h = R 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối trụ lớn nhất.
A. h = R 2
B. h = 2 R 3 3
C. h = R 3 3
D. h = R 2 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
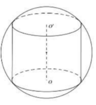
A. h = R 2
B. h = R 2 2
C. h = R 3 3
D. h = 2 R 3 3
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S). Thể tích khối nón (H) là V 1 thể tích phần còn lại của khối cầu là V 2 Giá trị lớn nhất của V 1 V 2 bằng:
A. 81 32
B. 76 32
C. 32 81
D. 32 76
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính r thay đổi, nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối nón lớn nhất
A. h = R 2
B. h = R 3
C. h = 4 R 3
D. h = 3 R 2
Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính R bằng
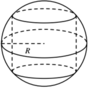
A. 4 πR 3 3 9
B. 8 πR 3 3 3
C. 8 πR 3 27
D. 8 πR 3 3 9