Đáp án A
Phương pháp: Thể tích khối trụ: 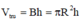 trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy.
trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy.
Cách giải: 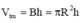 trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy
trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy
Đáp án A
Phương pháp: Thể tích khối trụ: 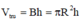 trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy.
trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy.
Cách giải: 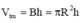 trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy
trong đó: B: diện tích đáy, h: chiều cao, R: bán kính đáy
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Thể tích V của khối trụ có bán kính đáy r = 4 và chiều cao h = 4 2 là:
A. V = 32 π
B. V = 32 2 π
C. V = 64 2 π
D. V = 128 π
Cho hình trụ có bán kính đáy r=2a và chiều cao h = a 3 . Tính thể tích V của khối trụ đã cho
A. V = π a 3 3
B. V = 5 π a 3 3
C. V = 2 π a 3 3
D. V = 4 π a 3 3
Cho khối nón có bán kính đáy r = 3, chiều cao h = 2 Tính thể tích V của khối nón.
A. V = 3 π 2 3
B. V = 3 π 2
C. V = 9 π 2 3
D. V = 9 π 2
Công thức tính thể tích khối trụ có bán kính đáy bằng R và chiều cao bằng h là
A. V = π R h
B. V = π R 2 h
C. V = 1 3 π R 2 h
D. V = π R h 2
Cho khối cầu (S) có tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
A. R 2
B. R 3 3
C. 4
D. 2
Khối trụ có bán kính đáy là r và độ dài chiều cao là h có thể tích bằng
A. 2 πr 2 h
B. πr 2 h
C. 1 3 πr 2 h
D. πr 2 h
Gọi l,h,R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối nón . Thể tích V của khối nón bằng
A. V = 1 3 π R 2 h
B. V = π R 2 h
C. V = π R 2 l
D. V = 1 3 π R 2 l
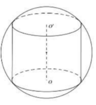
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
A. h = R 2
B. h = R 2 2
C. h = R 3 3
D. h = 2 R 3 3