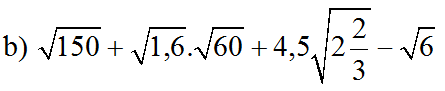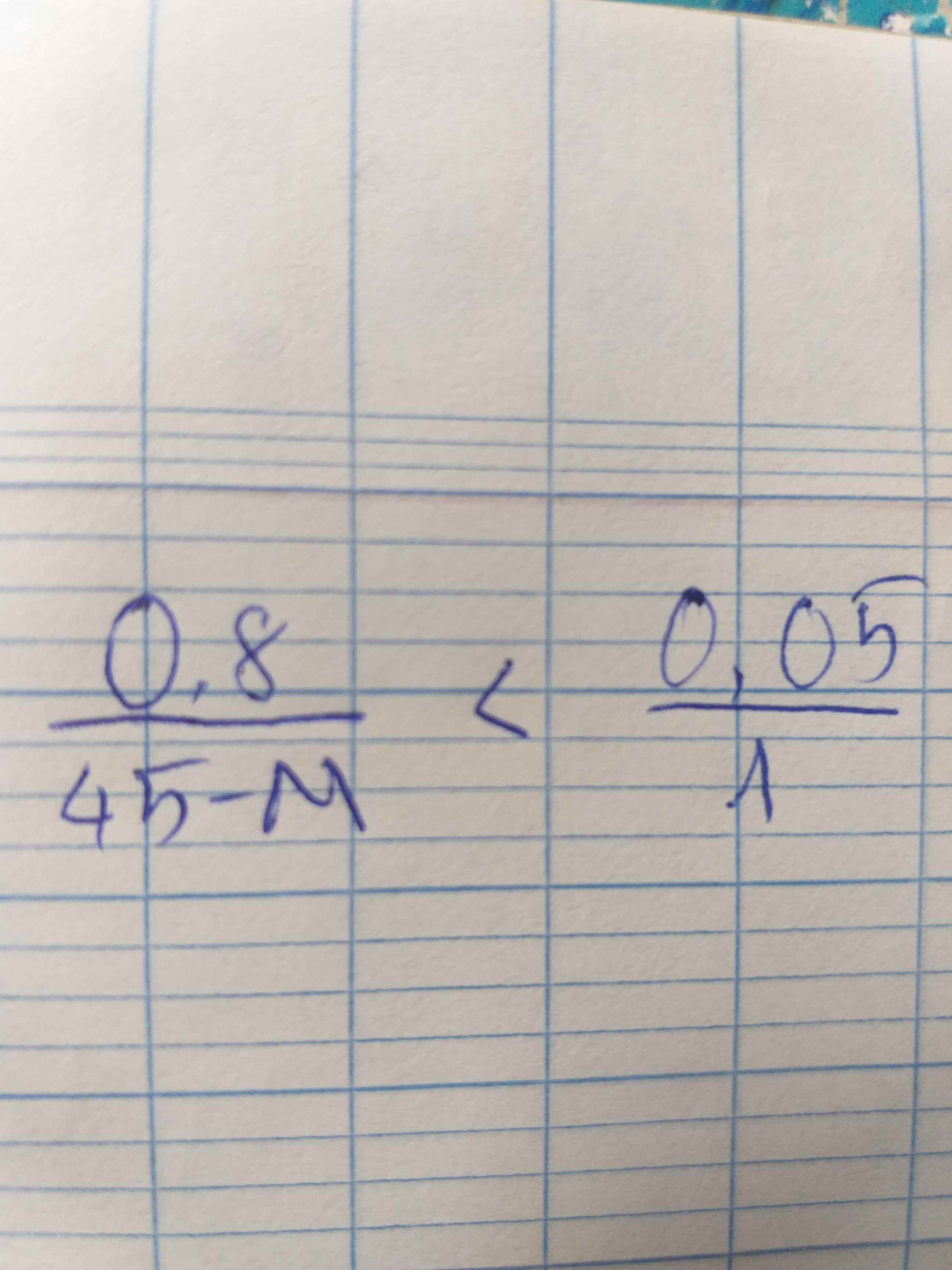2.2 Đề lỗi không dịch được
2.3
\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên ta có:
\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)
Thế vào bài toán:
\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)
\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)
(Bản thân câu này đề bài cũng rất dở)
a.
ĐKXĐ: \(x\ge\dfrac{1}{3}\)
\(9x^2-6x+1+2\sqrt{3x-1}+1=0\)
\(\Leftrightarrow\left(3x-1\right)^2+2\sqrt{3x-1}+1=0\)
Do \(\left\{{}\begin{matrix}\left(3x-1\right)^2\ge0\\2\sqrt{3x-1}\ge0\end{matrix}\right.\) ; \(\forall x\ge\dfrac{1}{3}\)
\(\Rightarrow\left(3x-1\right)^2+2\sqrt{3x-1}+1>0\)
Hay phương trình đã cho vô nghiệm