Question

Tất cả các giá trị thực của m để bất phương trình ( 3 m + 1 ) 18 x + ( 2 - m ) 6 x + 2 x < 0  có nghiệm đúng ∀ x > 0  là

A.  ( - ∞ ; 2 )

B.  - 2 ; - 1 3

C.  - ∞ ; - 1 3

D.  ( - ∞ ; - 2 ]

Answer 1

Đáp án D

BPT

( 3 m + 1 ) 9 x + ( 2 - m ) 3 x + 1 < 0  (1).

Đặt t = 3 x  ( Đk : t > 0 ).

BPT trở thành:

  ( 3 m + 1 ) t 2 + ( 2 - m ) 3 x + 1 < 0 ⇔ ( 3 t 2 - t ) m < - t 2 - 2 t - 1 (2).

Để BPT (1) nghiệm đúng  ∀ x > 0  

->BPT (2) nghiệm đúng   ∀ t > 1

nghiệm đúng  ∀ t > 1

( vì t > 1  nên 3 t 2 - t = t ( 3 t - 1 ) > 0 )

⇔ - t 2 - 2 t - 1 3 t 2 - t > m  (3) nghiệm đúng ∀ t > 1 .

* Xét f ( t ) = - t 2 - 2 t - 1 3 t 2 - t khi t > 1  :

lim x → ∞ f ( t ) = - 1 3  ;

  f ' ( t ) = ( - 2 t - 2 ) ( 3 t 2 - t ) - ( - t 2 - 2 t - 1 ) ( 6 t - 1 ) ( 3 t ² - t ) 2 = 7 t 2 + 6 t - 1 ( 3 t ² - t ) 2  .

Ta thấy : f ' ( t ) = 0 ⇔ t = - 1 t = 1 7 ⇒ f ' ( t ) > 0 ∀ t > 1

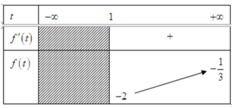
Từ BBT ta thấy: BPT (3) ) nghiệm đúng ∀ t > 1 ⇔ f ( t ) > m ∀ t > 1 ⇔ m ≤ - 2