Các câu hỏi tương tự
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
,
(
a
,
b
,
c
,
d
∈
ℝ
)
thỏa mãn
a
0
,
d
0
2018
,
a
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
với
a
,
b
,
c
,
d
∈
ℝ
,
a
0
và
d
2018
a
+
b
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d với a , b , c , d ∈ ℝ , a > 0 và d > 2018 a + b + c + d - 2018 < 0 . Số cực trị của hàm số y = f ( x ) - 2018 bằng
A. 3
B. 2
C. 1
D. 5
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Tìm tập xác định
D
ℝ
của hàm số
y
log
2
x
+
1
-
1
A.
D
(
-
∞
;
1
]
B.
D
3
;
+
∞...
Đọc tiếp
Tìm tập xác định D = ℝ của hàm số y = log 2 x + 1 - 1
A. D = ( - ∞ ; 1 ]
B. D = 3 ; + ∞
C. D = [ 1 ; + ∞ )
D. D = ℝ \ 3
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
x
4
−
4
x
2
+
3
. Dưới đây là lời giải của học sinh:* Bước 1: Tập xác định
D
ℝ
. Đạo hàm
y
8
x
3
−
8
x
.* Bước 2: Cho
y...
Đọc tiếp
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Tập
D
ℝ
k
π
2
k
∈
ℤ
là tập xác định của hàm số nào sau đây? A.
y
cot
x
B.
y
cot
2
x
C.
y
tan
x
D....
Đọc tiếp
Tập D = ℝ \ k π 2 k ∈ ℤ là tập xác định của hàm số nào sau đây?
A. y = cot x
B. y = cot 2 x
C. y = tan x
D. y = tan 2 x
Hàm số
y
ln
x
2
−
2
m
x
+
4
có tập xác định
D
ℝ
khi các giá trị của tham số m là A.
m
2
B.
m
−...
Đọc tiếp
Hàm số y = ln x 2 − 2 m x + 4 có tập xác định D = ℝ khi các giá trị của tham số m là
A. m < 2
B. m < − 2 m > 2
C. m = 2
D. − 2 < m < 2
Cho hàm số yf(x) xác định và liên tục trên tập
D
ℝ
{
-
1
}
và có bảng biến thiên:Dựa vào bảng biến thiên của hàm số yf(x) Khẳng định nào sau đây là khẳngđịnh sai? A. Giá trị nhỏ nhất của hàm số trên đoạn
[
1
;
8
]
bằng -2 B. Phương trình f(x)m có 3 nghiệm thực phân biệt khi x -2 C. Hàm số đạt cực tiểu tại x3 D. Hàm số nghịch biến trên khoảng
(
-...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên tập D = ℝ \ { - 1 } và có bảng biến thiên:
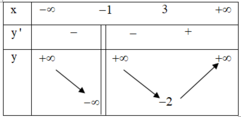
Dựa vào bảng biến thiên của hàm số y=f(x) Khẳng định nào sau đây là khẳng
định sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn [ 1 ; 8 ] bằng -2
B. Phương trình f(x)=m có 3 nghiệm thực phân biệt khi x > -2
C. Hàm số đạt cực tiểu tại x=3
D. Hàm số nghịch biến trên khoảng ( - ∞ ; 3 )
Cho hàm số
y
f
(
x
)
xác định và liên tục trên tập
D
ℝ
1
và có bảng biến thiênDựa vào bảng biến thiên của hàm số
y
f
x
. Khẳng định nào sau đây là sai? A. Phương trình
f
x
m
có 3 nghiệm thực phân biệt khi x -2 B. Giá trị nhỏ nhất của hàm s...
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên tập D = ℝ \ 1 và có bảng biến thiên
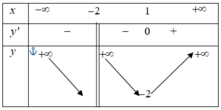
Dựa vào bảng biến thiên của hàm số y = f x . Khẳng định nào sau đây là sai?
A. Phương trình f x = m có 3 nghiệm thực phân biệt khi x > -2
B. Giá trị nhỏ nhất của hàm số trên đoạn 0 ; 6 là -2
C. Hàm số đạt cực tiểu tại x = 1
D. Hàm số nghịch biến trên khoảng − ∞ ; 1
Cho
f
x
là hàm đa thức thỏa mãn
f
x
-
x
f
1
-
x
x
4
-
5
x
3
+
12
x
2
-
4
∀
x
∈
ℝ
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất...
Đọc tiếp
Cho f x là hàm đa thức thỏa mãn f x - x f 1 - x = x 4 - 5 x 3 + 12 x 2 - 4 ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f x trên tập D = x ∈ ℝ | x 4 - 10 x 2 + 9 ≤ 0 . Giá trị của 21 m + 6 M + 2019 bằng
A. 2235.
B. 2319.
C. 3045.
D. 3069.



