Các câu hỏi tương tự
Cho hàm số yf(x). Đồ thị hàm số yf’(x) như hình vẽ. Đặt
g
(
x
)
3
f
(
x
)
-
x
3
+
3
x
-
m
, với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với
∀
x
∈
-
3
;
3...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f’(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) - x 3 + 3 x - m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g(x)≥0 nghiệm đúng với ∀ x ∈ - 3 ; 3 là
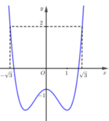
A. m < 3 f 3
B. m > 3 f 3
C. m ≤ 3 f 3
D. m ≥ 3 f 3
Tập nghiệm của bất phương trình log 2 x - log x 3 + 2 ≥ 0 là S = ( a ; b ] ∪ [ c ; + ∞ ) thì a + b + c là:
A. 10
B. 100
C. 110
D. 2018
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình
log
x
(
5
x
2
-
8
x
+
3
)
2
đều là nghiệm của bất phương trình
x
2
-
2
x
-
a
4
+
1
≥
0
.
Khi đó:...
Đọc tiếp
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình log x ( 5 x 2 - 8 x + 3 ) > 2 đều là nghiệm của bất phương trình x 2 - 2 x - a 4 + 1 ≥ 0 . Khi đó:
A. S = - 10 5 ; 10 5 .
B. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞
C. S = - 10 5 ; 10 5 .
D. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞ .
Biết tập nghiệm S của bất phương trình
log
π
6
log
3
x
-
2
0
là khoảng (a;b). Tính b - a. A. 2 B. 4 C. 3 D. 5
Đọc tiếp
Biết tập nghiệm S của bất phương trình log π 6 log 3 x - 2 > 0 là khoảng (a;b). Tính b - a.
A. 2
B. 4
C. 3
D. 5
Nghiệm của bất phương trình
2
x
+
2
-
x
-
3
0
là A.
log
2
3
-
5
2
x
log
2
3
+
5...
Đọc tiếp
Nghiệm của bất phương trình 2 x + 2 - x - 3 < 0 là
A. log 2 3 - 5 2 < x < log 2 3 + 5 2
B. x < log 2 3 - 5 2 , x > log 2 3 + 5 2
A. log 2 3 - 5 2 < x < log 2 3 + 5 2
D. x < log 2 4 - 5 2 , x > log 2 4 + 5 2
Trong mặt phẳng tọa độ cho Oxy bốn điểm A(3;-5), B(-3;3) ,C(-1;-2) ,D(5;-10). Hỏi G
1
3
;
-
3
là trọng tâm của tam giác nào dưới đây? A. ABC. B. BCD. C. ACD. D. ABD
Đọc tiếp
Trong mặt phẳng tọa độ cho Oxy bốn điểm A(3;-5), B(-3;3) ,C(-1;-2) ,D(5;-10). Hỏi G 1 3 ; - 3 là trọng tâm của tam giác nào dưới đây?
A. ABC.
B. BCD.
C. ACD.
D. ABD
Tập nghiệm S của bất phương trình
log
2
x
+
2
≤
0
là A.
S
0
;
-
1
B.
S
-
1
;
+
∞
C.
S...
Đọc tiếp
Tập nghiệm S của bất phương trình log 2 x + 2 ≤ 0 là
A. S = 0 ; - 1
B. S = - 1 ; + ∞
C. S = - 2 ; - 1
D. S = - 2 ; + ∞
Cho hàm số f(x)-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình:
f
(
x
)
≥
0
là
Đọc tiếp
Cho hàm số f(x)=-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình: f ' ( x ) ≥ 0 là
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình:
2
.
4
x
-
5
.
2
x
+
2
≤
0
có dạng
S
a
;
b
Tính b - a A. 1 B.
5
2
C. 2 D.
3
2
Đọc tiếp
Tập nghiệm của bất phương trình: 2 . 4 x - 5 . 2 x + 2 ≤ 0 có dạng S = a ; b Tính b - a
A. 1
B. 5 2
C. 2
D. 3 2
Tập nghiệm của bất phương trình
3
2
x
+
2
-
2
.
6
x
-
7
.
4
x
0
là: A.
S
1
;
+
∞
B. S (-1;0) C.
S...
Đọc tiếp
Tập nghiệm của bất phương trình 3 2 x + 2 - 2 . 6 x - 7 . 4 x > 0 là:
A. S = 1 ; + ∞
B. S = (-1;0)
C. S = 0 ; + ∞
D. S = ( - ∞ ; - 1 )



