Để hàm số đồng biến trên - ∞ ; + ∞ khi và chỉ khi

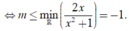
Chọn C.
Để hàm số đồng biến trên - ∞ ; + ∞ khi và chỉ khi

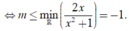
Chọn C.
Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = x 2 + 3 - m ( x + 1 ) đồng biến trên khoảng ( - ∞ ; + ∞ )
A. [ 1 ; + ∞ )
B. [ - 1 ; 1 ]
C. ( - ∞ ; - 1 ]
D. ( - ∞ ; 1 )
Tập hợp tất cả các giá trị thực của tham số thực m để hàm số y = l n ( x 2 + 1 ) - m x + 1 đồng biến trên R
A. [-1;1].
B. (-1;1)
C. (-∞;-1]
D.(- ∞;-1)
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = x 2 + 1 - m x - 1 đồng biến trên khoảng ( - ∞ ; + ∞ ) .
A. - ∞ ; 1
B. [ 1 ; + ∞ )
C. - 1 ; 1
D. - ∞ ; - 1
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = x 2 + 1 − mx − 1 đồng biến trên khoảng − ∞ ; + ∞ ?
A. − ∞ ; 1 .
B. 1 ; + ∞ .
C. − 1 ; 1 .
D. − ∞ ; − 1 .
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln x 2 + 1 − m x + 1 đồng biến trên khoảng − ∞ ; + ∞
A. − ∞ ; − 1
B. − 1 ; 1
C. − 1 ; 1
D. − ∞ ; − 1
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = x 3 - ( m + 1 ) x 2 + 3 x + 1 đồng biến trên khoảng từ ( - ∞ ; + ∞ )
A. ( - ∞ ; - 4 ) ∪ ( 2 ; + ∞ )
B. [-4;2]
C. ( - ∞ ; - 4 ] ∪ [ 2 ; + ∞ )
D. (-4;2)
Tập hợp tất cả các giá trị của tham số m để hàm số y = x 3 − m x 2 − m − 6 x + 1 đồng biến trên khoảng (0;4)
A. − ∞ ; 6
B. − ∞ ; 3
C. − ∞ ; 3
D. [3;6]
Cho hàm số y = x 3 - ( m + 1 ) x 2 + 3 x + 1 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng ( - ∞ ; + ∞ ) Tìm số phần tử của S
A. 7
B. 6
C. Vô số
D. 5
Tìm tập hợp tất cả các tham số m để hàm số y = x 3 – m x 2 + ( m – 1 ) x + 1 đồng biến trên khoảng (1; 2)
A. m ≤ 11 3
B. m < 11 3
C. m ≤ 2
D. m < 2