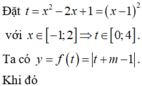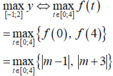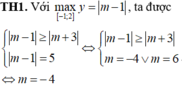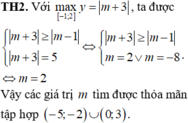Các câu hỏi tương tự
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
3
+
(
k
2
-
k
+
1
)
x
trên đoạn [-1;2]. Khi k thay đổi trên
ℝ
, giá trị nhỏ nhất c...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + ( k 2 - k + 1 ) x trên đoạn [-1;2]. Khi k thay đổi trên ℝ , giá trị nhỏ nhất của M - m bằng.
Cho hàm số 
. Tìm tất cả các giá trị của tham số thực m để hàm số đạt giá trị lớn nhất tại điểm x=1
A. Không có giá trị m
B. m = 1
C. m = 2
D. m = -3
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số nghịch biến trên
D
[
2
;
+
∞
)
. A. B. C. D.
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 
nghịch biến trên
D
=
[
2
;
+
∞
)
.
A. 
B. 
C. 
D. 
cho hàm số \(\dfrac{-x+2}{x-1}\) có đồ thị (C) và điểm A(a;1) . Gọi S là tập hợp tất cả các giá trị thực củ tham số a để có đúng 1 tiếp tuyến của (C) đi qua A. Tổng tất cả các giá trị của S là
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]
Với tất cả các giá trị thực nào của tham số m thì hàm số
y
x
3
-
3
(
m
+
1
)
x
2
+
3
m
(
m
+
2...
Đọc tiếp
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x 3 - 3 ( m + 1 ) x 2 + 3 m ( m + 2 ) x nghịch biến trên đoạn [0;1]?
A. - 1 ≤ m ≤ 0
B. - 1 < m < 0
C. m ≥ - 1
D. m ≤ 0
Tìm các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số rên đoạn [-2;-1] bằng 4 ? A.
m
±
3
B.
m
∈
∅
C.
m
±
26...
Đọc tiếp
Tìm các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số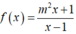 
rên đoạn [-2;-1] bằng 4 ?
A. m = ± 3
B. m ∈ ∅
C. m = ± 26 2
D. m = ± 9
tìm tổng tất cra các giá trị của tham số thực m để hàm số y=|mx-1|-x^2 có giá trị lớn nhất bằng 10/8
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số
y
x
2
+
m
4
-
x
2
+
m
-
7
có điểm chung với trục hoành là [a;b] (với a;b
∈...
Đọc tiếp
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 2 + m 4 - x 2 + m - 7 có điểm chung với trục hoành là [a;b] (với a;b ∈ ℝ ). Tính giá trị của S = 2a + b.
A. S = 19 3
B. S = 7
C. S = 5
D. S = 23 3