Các câu hỏi tương tự
Số phức z = a + bi(a, b thuộc R) là số thuần ảo khi và chỉ khi
A. a = 0; b ≠ 0
B. a ≠ 0; b = 0
C. a = 0
D. b = 0
Cho hai số phức z a + bi và z’ a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
Đọc tiếp
Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
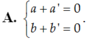
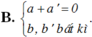
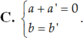
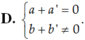
Cho số phức z a + bi với
a
,
b
∈
R
. Nếu z là số thuần ảo thì đâu là khẳng định đúng? A. a 0 B. a 0 và
b
≠
0
C. b 0 D. b 0 và
a
≠
0
Đọc tiếp
Cho số phức z = a + bi với a , b ∈ R . Nếu z là số thuần ảo thì đâu là khẳng định đúng?
A. a = 0
B. a = 0 và b ≠ 0
C. b = 0
D. b = 0 và a ≠ 0
Cho hai số phức
z
-
2
+
5
i
,
z
a
+
b
i
(
a
,
b
∈
R
)
Xác định a,b để z + z’ là một số thuần ảo
Đọc tiếp
Cho hai số phức z = - 2 + 5 i , z ' = a + b i ( a , b ∈ R ) Xác định a,b để z + z’ là một số thuần ảo
![]()
![]()
![]()
![]()
Cho số phức z = ( a + b i ) 2 . Để là số thuần ảo thì
A. a = b = 1
B. a = b = -1
C. a = b = 0
D. |a| = |b|
Cho số phức z(1-2i)(4-3i)-2+8i. Cho các phát biểu sau: (1) Modun của z là một số nguyên tố (2) z có phần thực và phần ảo đều âm (3) z là số thuần thực (4) Số phức liên hợp của z có phần ảo là 3i Số phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Gọi số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn |z-1| = 1 và (1+i)( z ¯ -1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a, b bằng
A. a.b = 1
B. a.b = 2
C. a.b = -2
D. a.b = -1
Gọi số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
)
thỏa mãn
z
-
1
1
và...
Đọc tiếp
Gọi số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 1 = 1 và ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab=-2
B. ab=2
C. ab=1
D. ab=-1
Gọi số phức za+bi (a,b
∈
ℝ
) thỏa mãn
z
-
1
1
v
à
(
1
+
i
)
(
z
¯
-
1
)
có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng:
Đọc tiếp
Gọi số phức z=a+bi (a,b ∈ ℝ ) thỏa mãn z - 1 = 1 v à ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng:
![]()
![]()
![]()
![]()



