Các câu hỏi tương tự
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là
A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Gọi M là giao điểm của đồ thị hàm số
y
x
+
1
x
−
2
với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là: A.
3
y
+
x
+
1
0
B.
3
y
+
x
−
1
0
C.
3...
Đọc tiếp
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là:
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Gọi M là giao điểm của đồ thị hàm số
y
x
+
1
x
−
2
với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là A.
3
y
+
x
+
1
0
B.
3
y
+
x
−
1
0
C.
3...
Đọc tiếp
Gọi M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm M là
A. 3 y + x + 1 = 0
B. 3 y + x − 1 = 0
C. 3 y − x + 1 = 0
D. 3 y − x − 1 = 0
Tìm số giao điểm của đồ thị hàm số y = ( x − 2 ) ( x 2 + 3 x + 3 ) với trục hoành.
A. 2
B. 0
C. 1
D. 3
Biết đồ thị hàm số bậc bốn yf(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số yg(x) [f’(x)]2 – f(x). f’’(x) và trục hoành A. 4 B. 0. C. 6. D. 2.
Đọc tiếp
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành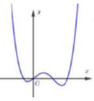
A. 4
B. 0.
C. 6.
D. 2.
Hoành độ giao điểm của đồ thị hàm số y = x 4 - 3 x 2 - 4 và trục hoành là
A. -1;1
B. -2;-1;2
C. -2;2
D. -2;-1;1;2
Hoành độ giao điểm của đồ thị hàm số
y
x
4
−
3
x
2
−
4
và trục hoành là A. −1; 1 B. −2; 2 C. −2; −1; 1; 2 D. −2; −1; 2
Đọc tiếp
Hoành độ giao điểm của đồ thị hàm số y = x 4 − 3 x 2 − 4 và trục hoành là
A. −1; 1
B. −2; 2
C. −2; −1; 1; 2
D. −2; −1; 2
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết...
Đọc tiếp
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.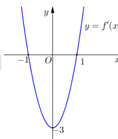
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4
Biết đồ thị hàm số
f
x
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S
1
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi
S
2
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết...
Đọc tiếp
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Số giao điểm của đồ thị hàm số
y
x
-
1
x
2
+
2
x
-
3
với trục hoành là A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Số giao điểm của đồ thị hàm số y = x - 1 x 2 + 2 x - 3 với trục hoành là
A. 1
B. 2
C. 3
D. 0