Question

Số giá trị của m để giá trị lớn nhất của hàm số: \(y=\left|x^2-2x+m^2+2m\right|\) trên [-1;2] bằng 2 là?

Answer 1

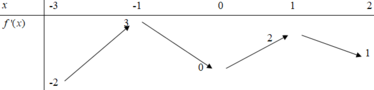
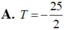Đặt \(f\left(x\right)=x^2-2x+m^2+2m\)

Ta có: \(max_{\left[-1;2\right]}y=2\Leftrightarrow\left\{{}\begin{matrix}min_{\left[-1;2\right]}f\left(x\right)=-2\\max_{\left[-1;2\right]}f\left(x\right)=2\end{matrix}\right.\)

Bảng biến thiên của hàm số f(x):

Để ý \(\left\{{}\begin{matrix}min_{\left[-1;2\right]}f\left(x\right)=m^2+2m-1\\max_{\left[-1;2\right]}f\left(x\right)=m^2+2m+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m^2+2m-1=-2\\m^2+2m+3=2\end{matrix}\right.\Rightarrow m=-1\)

Vậy chỉ có duy nhất giá trị m=-1 thì hàm số trên đạt GTLN trên [-1;2]