Question

Số giá trị của m để giá trị lớn nhất của hàm số \(y=\left|x^2-2x+m^2+2m+2\right|\) trên [-1;2] bằng 2 là?

Answer 1

Đặt \(f\left(x\right)=x^2-2x+m^2+2m+2\)

\(f'\left(x\right)=2x-2\)

\(f'\left(x\right)=0\Rightarrow x=1\)

bbt của \(f\left(x\right)\) là

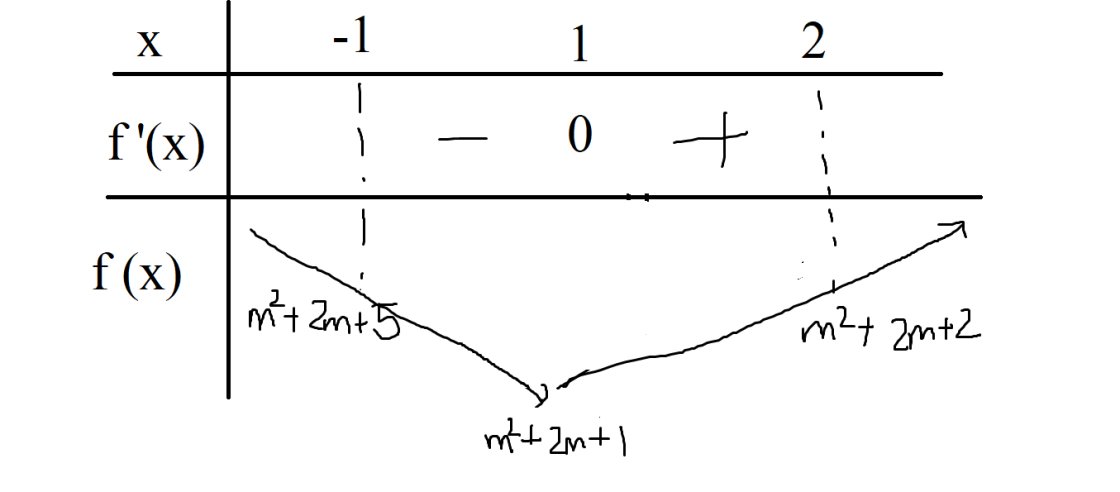
bbt của hàm số \(y=\left|f\left(x\right)\right|\) sẽ là bbt của \(f\left(x\right)\) giữ nguyên phần nằm trên trục hoành và lấy đối xứng qua trục hoành phần đồ thị nằm dưới trục hoành

Vì \(f\left(1\right)=m^2+2m+1=\left(m+1\right)^2\ge0\) nên bbt của \(y=\left|f\left(x\right)\right|\) cũng giống với bbt của \(y=f\left(x\right)\)

Dựa và bbt thì \(y_{max\left[-1,2\right]}=y\left(-1\right)=m^2+2m+5\Rightarrow m^2+2m+5=2\)

\(\Rightarrow\) không có m thỏa đề