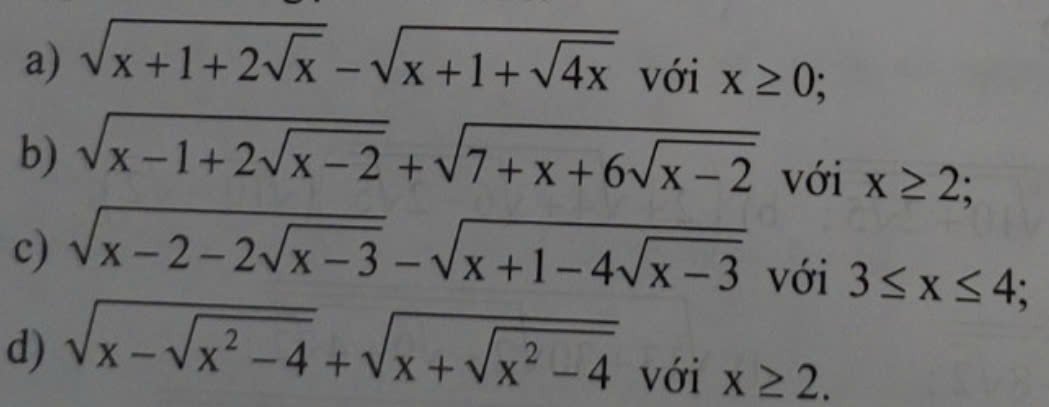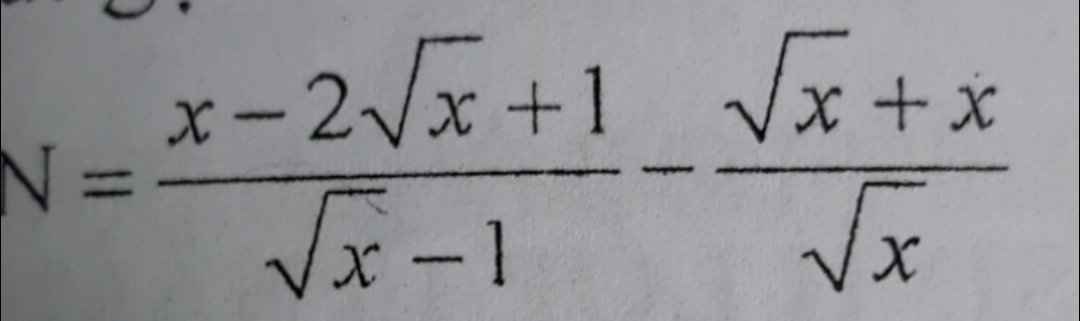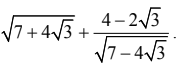a.
\(=\sqrt{x+1+2\sqrt{x}}-\sqrt{x+1+2\sqrt{x}}\)
\(=0\) (chắc đề ghi nhầm, \(\sqrt{x+1-2\sqrt{x}}\) đúng hơn)
b.
\(=\sqrt{x-2+2\sqrt{x-2}+1}+\sqrt{x-2+6\sqrt{x-2}+9}\)
\(=\sqrt{\left(\sqrt{x-2}+1\right)^2}+\sqrt{\left(\sqrt{x-2}+3\right)^2}\)
\(=\left|\sqrt{x-2}+1\right|+\left|\sqrt{x-2}+3\right|\)
\(=\sqrt{x-2}+1+\sqrt{x-2}+3\)
\(=2\sqrt{x-2}+4\)
c.
\(=\sqrt{x-3-2\sqrt{x-3}+1}-\sqrt{x-3-4\sqrt{x-3}+4}\)
\(=\sqrt{\left(\sqrt{x-3}-1\right)^2}-\sqrt{\left(\sqrt{x-3}-2\right)^2}\)
\(=\left|\sqrt{x-3}-1\right|-\left|\sqrt{x-3}-2\right|\) (1)
Do \(3\le x\le4\Rightarrow0\le\sqrt{x-3}\le1\)
Nên (1) trở thành:
\(=\left(1-\sqrt{x-3}\right)-\left(2-\sqrt{x-3}\right)\)
\(=-1\)
d.
Đặt \(D=\sqrt{x-\sqrt{x^2-4}}+\sqrt{x+\sqrt{x^2-4}}\Rightarrow D\ge0\)
\(D^2=2x+2\sqrt{\left(x-\sqrt{x^2-4}\right)\left(x+\sqrt{x^2-4}\right)}\)
\(D^2=2x+2\sqrt{x^2-\left(x^2-4\right)}\)
\(D^2=2x+4\)
\(\Rightarrow D=\sqrt{2x+4}\)