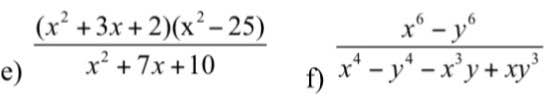\(e,\dfrac{\left(x^2+3x+2\right)\left(x^2-25\right)}{x^2+7x+10}=\dfrac{\left[\left(x^2+x\right)+\left(2x+2\right)\right]\left(x-5\right)\left(x+5\right)}{\left(x^2+2x\right)+\left(5x+10\right)}=\dfrac{\left[x\left(x+1\right)+2\left(x+1\right)\right]\left(x-5\right)\left(x+5\right)}{x\left(x+2\right)+5\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)\left(x-5\right)\left(x+5\right)}{\left(x+2\right)\left(x+5\right)}=\left(x+1\right)\left(x-5\right)\)
\(f,\dfrac{x^6-y^6}{x^4-y^4-x^3y+xy^3}=\dfrac{\left(x^3-y^3\right)\left(x^3+y^3\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)-xy\left(x^2-y^2\right)}=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)\left(x+y\right)\left(x^2-xy+y^2\right)}{\left(x-y\right)\left(x+y\right)\left(x^2-xy+y^2\right)}=x^2+xy+y^2\)