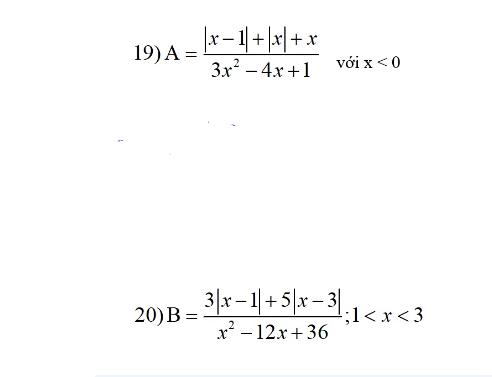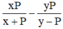Question

Rút gọn biểu thức:

Answer 1

\(A=\dfrac{\left|x-1\right|+\left|x\right|+x}{3x^2-4x+1}=\dfrac{1-x-x+x}{3x^2-3x-x+1}=\dfrac{1-x}{3x\left(x-1\right)-\left(x-1\right)}=-\dfrac{x-1}{\left(3x-1\right)\left(x-1\right)}=\dfrac{1}{1-3x}\)

Answer 2

\(B=\dfrac{3\left|x-1\right|+5\left|x-3\right|}{x^2-12x+36}=\dfrac{3\left(x-1\right)-5\left(x-3\right)}{\left(x-6\right)^2}=\dfrac{3x-3-5x+15}{\left(x-6\right)^2}=\dfrac{-2x+12}{\left(x-6\right)^2}=\dfrac{-2\left(x-6\right)}{\left(x-6\right)^2}=-\dfrac{2}{x-6}=\dfrac{2}{6-x}\)