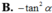Các câu hỏi tương tự
Cho
α
là góc thỏa
sin
α
1
4
. Tính giá trị của biểu thức
A
sin
4
α
+
2
sin
2
α
cos
α
A.
255
128
B.
225
182
C.
255
182...
Đọc tiếp
Cho α là góc thỏa sin α = 1 4 . Tính giá trị của biểu thức A = sin 4 α + 2 sin 2 α cos α
A. 255 128
B. 225 182
C. 255 182
D. 255 128
Cho góc
α
thỏa mãn
5
sin
2
α
-
6
cos
α
0
và
0
α
π
2
.Tính giá trị của biểu thức: A
cos
(
π
2
-
α
)
+
sin
(
2015
π
-
α
)
-
c
o...
Đọc tiếp
Cho góc α thỏa mãn 5 sin 2 α - 6 cos α = 0 và 0 < α < π 2 .
Tính giá trị của biểu thức: A = cos ( π 2 - α ) + sin ( 2015 π - α ) - c o t ( 2016 π + α ) .
A. - 2 15
B. 4 15
C. 1 15
D. - 3 5
Biết
sin
α
-
cos
α
m
. Tính
sin
3
α
-
cos
3
α
: A.
3
-
m
2
B.
m
3
-
m...
Đọc tiếp
Biết sin α - cos α = m . Tính sin 3 α - cos 3 α :
A. 3 - m 2
B. m 3 - m 2 2
C. m 3 - m 2
D. 3 - m 2 2
Cho
α
,
β
thỏa mãn
sin
α
+
sin
β
2
2
;
cos
α
+
cos
β
6
2
. Tính
cos
α...
Đọc tiếp
Cho α , β thỏa mãn sin α + sin β = 2 2 ; cos α + cos β = 6 2 . Tính cos α - β .
A. cos α - β = 0
B. cos α - β = 2 2
C. cos α - β = 3 2
D. cos α - β = 1 2
Cho hình chóp S.ABCD có đáy ABC vuông tại B, (SAC) vuông góc với (ABC), biết
SB
SC
a
,
SA
BC
a
3
. Gọi
α
là góc tạo bởi SA và (SBC). Tính
sin
α
A.
sin...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABC vuông tại B, (SAC) vuông góc với (ABC), biết SB = SC = a , SA = BC = a 3 . Gọi α là góc tạo bởi SA và (SBC). Tính sin α
A. sin α = 2 13
B. sin α = 3 13
C. sin α = 1 3 13
D. sin α = 1 2 13
Tìm GTLN và GTNN của hàm số
c
o
s
α
2
sin
2
α
+
sin
α
-
3
0
là: A.
m
a
x
y
1...
Đọc tiếp
Tìm GTLN và GTNN của hàm số c o s α 2 sin 2 α + sin α - 3 = 0 là:
A. m a x y = 1 m i n y = - 1 11
B. m a x y = 2 m i n y = - 2 11
C. m a x y = 2 m i n y = 2 11
D. m a x y = 1 m i n y = 1 11
Cho
a
∈
(
0
;
π
2
]
và thỏa mãn
c
o
s
α
2
sin
2
α
+
sin
α
-
3
0
. Tính giá trị của
c
o
t
α
2
A. y sin2x B. y 2cosx + 3 C. y sinx + cosx D....
Đọc tiếp
Cho a ∈ ( 0 ; π 2 ] và thỏa mãn c o s α 2 sin 2 α + sin α - 3 = 0 . Tính giá trị của c o t α 2
A. y = sin2x
B. y = 2cosx + 3
C. y = sinx + cosx
D. y = tan2x + cotx
Cho
a
∈
(
0
;
π
2
]
và thỏa mãn
c
o
s
α
2
sin
2
α
+
sin
α
-
3
0
. Tính giá trị của
c
o
t
α
2
A.
1
2...
Đọc tiếp
Cho a ∈ ( 0 ; π 2 ] và thỏa mãn c o s α 2 sin 2 α + sin α - 3 = 0 . Tính giá trị của c o t α 2
A. 1 2
B. 3 2
C. 4
D. 1
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD 600 , SASBSD
a
3
2
. Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng A.
1
3
B.
2
3
C.
5
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD = 600 , SA=SB=SD= a 3 2 . Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
B
C
a
3
,
S
A
a
và SA vuông góc với đáy ABCD. Tính
sin
α
, với
α
là góc tạo bởi giữa đường thẳng BD và mặt phẳng
S
B
C
. A.
sin...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng S B C .
A. sin α = 7 8
B. sin α = 3 2
C. sin α = 2 4
D. sin α = 3 5