Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
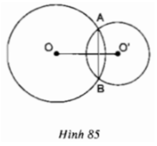
a) Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
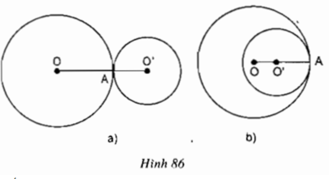
b) Quan sát hình 86, hãy dự đoán về vị trí của điểm A đối với đường nối tâm OO’.
Cho hình thang ABCD (AB//CD). Gọi E, F là trung điểm của BD và AC
a) Chứng minh rằng EF//CD.
b) Đường thẳng qua E vuông góc với AD cắt đường thẳng qua F vuông góc với BC tại G. Chứng minh rằng điểm G nằm trên đường trung trực của đoạn thẳng CD.
1/ cho tam giác ABC cân đỉnh A. đường cao BE;CF cắt nhau tại H. D là trung điểm của BC.
a/ chứng minh 4 điểm B;F;E;C cùng một đường tròn
b/ 4 điểmB;H;E;C có thuộc đường tròn không? vì sao?
c/ xác định tâm đường tròn đi qua 4 điểm A;F;B;C
d/ có thể khẳng định điểm B nằm ngoài đường tròn đi qua 4 điểm A;F;B;C không?
e/ chứng minh EF < BC
2/ cho ( O;R ); ( O';R') cắt nhau tại A;B (O;O' thuộc 2 nửa mặt phẳng bờ AB). trong cùng một nửa mặt phẳng bờ OO' vẽ hai bán kính OC; O'D sao cho OC//O'D. gọi E là điểm đối xứng của B qua OO'
a/ chứng minh AOBO' là hình thoi
b/ chứng minh AB;OO';CE đồng quy
c/ chứng minh A là trực tâm của tam giác BCD
Tam giác ABC có phân giác trong AD. (O), (O') là đường tròn ngoại tiếp tam giác ABD, ACD. AD cắt hai tiếp tuyến chung của (O), (O') tại P, Q. L là giao điểm của AD với trung trực của BC.
a) Chứng minh BC, hai tiếp tuyến chung và OO' đồng quy.
b) Gọi M, H là tiếp điểm của (O), (O') với các tiếp tuyến chung. Chứng minh MH, OO', AB đồng quy.
c) Chứng minh SA là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
d) Chứng minh CB là tiếp tuyến của (O), CL là tiếp tuyến của (O').
e) PQ^2=AB.AC.
Cho hình chữ nhật abcd.gọi M,N,K lần lượt là trung diểm AH,BH,CD trong đó H là hình chiếu vuông góc của B lên AC
1 chứng minh rằng tứ giác MNCK là hình bình hành.
2 chứng minh rằng N là trực tâm tam giác BCM.
3 chứng minh rằng tứ giác BMKC nội tiếp
4 Đường tròn nội tiếp tứ giác BMKC cắt AB tại I( I khác B ).Chứng mình rằng 2AI^2=AM.AC
Cho đường tròn (0,3cm). Từ điểm A nằm ngoài đường tròn kẻ tâm tiếp tuyến AB (B là tiếp diễn) sao cho AOB=30° a) tính OA b) Chứng minh rằng: AD là tiếp tuyến của đường tròn (O) c) Chứng minh rằng: OA là đường trung trực BD
Cho tam giác ABC nhọn . Các đường cao AD , BE , CF gặp nhau tại H . Gọi M, N , P là trung điểm của BC , CA , AB ; I , K ,F là trung điểm của HB , HC , HA
a. Chứng minh rằng : IKNP là hình chữ nhật
b. Chứng mình rằng : NI , KP , NI , QM đồng quy
c. Chứng minh : 9 điểm : chân 3 đường cao , trung điểm của 3 cạnh , trung điểm của 3 đoạn thẳng từ trực tâm đến các đỉnh cùng nằm trên 1 đường tròn , đường tròn Ơle
Cho hình vuông ABCD. Vẽ điểm M thỏa BM vuông góc với BD và M không thuộc các đường thẳng DA và DC. Trung trực của DM cắt AB và BC lần lượt tại F và E. Gọi O là tâm của hình vuông ABCD và I là trung điểm của DM.
1. Chứng minh bốn điểm A, O, I,Cthẳng hàng.
2. Chứng minh rằng góc AFD = góc DEC.
3. Chứng minh rằng DEMF là hình vuông.
Cho \(\Delta ABC\)vuông tại A. I là trung điểm của cạnh BC, D là một điểm bất kỳ trên cạnh BC. Đường trung trực của AD cắt các đường trung trực của AB, AC theo thứ tự tại E và F.
a) Chứng minh rằng: 5 điểm A, E, I, D, F cùng thuộc một đường tròn
b) Chứng minh rằng: AE.AC=AF.AB
c) Cho AC=b; AB=c. Tìm GTNN của diện tích tam giác AEF theo b, c