a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
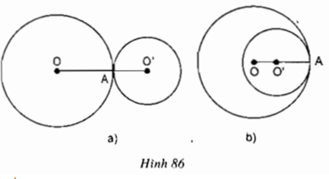
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
Quan sát hình 86, hãy dự đoán về vị trí của điểm A đối với đường nối tâm OO’.
Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
QUẢNG CÁO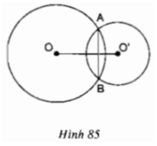
Cho hình 88.
a) Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MNQP là hình thang cân.
1/ cho tam giác ABC cân đỉnh A. đường cao BE;CF cắt nhau tại H. D là trung điểm của BC.
a/ chứng minh 4 điểm B;F;E;C cùng một đường tròn
b/ 4 điểmB;H;E;C có thuộc đường tròn không? vì sao?
c/ xác định tâm đường tròn đi qua 4 điểm A;F;B;C
d/ có thể khẳng định điểm B nằm ngoài đường tròn đi qua 4 điểm A;F;B;C không?
e/ chứng minh EF < BC
2/ cho ( O;R ); ( O';R') cắt nhau tại A;B (O;O' thuộc 2 nửa mặt phẳng bờ AB). trong cùng một nửa mặt phẳng bờ OO' vẽ hai bán kính OC; O'D sao cho OC//O'D. gọi E là điểm đối xứng của B qua OO'
a/ chứng minh AOBO' là hình thoi
b/ chứng minh AB;OO';CE đồng quy
c/ chứng minh A là trực tâm của tam giác BCD
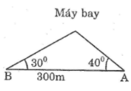
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là 40 ° và tại vị trí B là 30 ° (hình bên). Hãy tìm độ cao của máy bay.
Giải bài :Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Gọi P là điểm đối xứng với M qua OO', Q là điểm đối xứng với N qua OO'. Chứng minh rằng: a/ MNPQ là hình thang cân.
Cho 2 đường tròn O và O(1) ở ngoài nhau. Đường nối tâm OO(1) cắt đường tròn taamO và đường tròn tâm O(1) tại các điểm A B C D theo thứ tự trên đường thẳng. Kẻ tiếp tuyến chung ngoài EF ( E thuộc dt tâm O, F thuộc dt tâm O(1). Gọi M là giao điểm của AE và DM, N là giao điểm của EB và FC. Chứng minh rằng:
- Tứ giác MENF là hình chữ nhật
- MN vuông góc với AD
- ME.MA=MF.MD
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng: AB ⊥ KB