Question

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MNQP là hình thang cân.

Answer 1

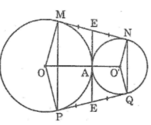
Vì M và P đối xứng qua trục OO’ nên OO’ là đường trung trực của MP

Suy ra: OP = OM

Khi đó P thuộc (O) và MP ⊥ OO’    (1)

Vì N và Q đối xứng qua trục OO’ nên OO’ là đường trung trực của NQ

Suy ra: O’N = O’Q

Khi đó Q thuộc (O’) và NQ ⊥ OO’    (2)

Từ (1) và (2) suy ra: MP // NQ

Tứ giác MNQP là hình thang

Vì OO’ là đường trung trực của MP và NQ nên OO’ đi qua trung điểm hai đáy hình thang MNQP, OO’ đồng thời cũng là trục đối xứng của hình thang MNQP nên MNQP là hình thang cân.