Question

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MN + PQ = MP + NQ.

Answer 1

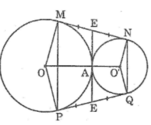
Kẻ tiếp tuyến chung tại A cắt MN tại E và PQ tại F

Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có:

EM = EA và FP = FA

Trong đường tròn (O’), theo tính chất hai tiếp tuyến cắt nhau, ta có:

EN = EA và FQ = FA

Suy ra: EM = EA = EN = (1/2).MN

FP = FA = FQ = (1/2).PQ

Suy ra : MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF    (9)

Vì EF là đường trung bình của hình thang MNQP nên :

EF = (MP + NQ)/2 hay MP + NQ = 2EF    (10)

Từ (9) và (10) suy ra: MN + PQ = MP + NQ