Ta có: MN ⊥ OM (tính chất tiếp tuyến)
Suy ra: QP ⊥ OP tại P
Vậy PQ là tiếp tuyến của đường tròn (O).
Ta có: MN ⊥ O’N (tính chất tiếp tuyến)
Suy ra: QP ⊥ O’Q tại Q
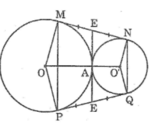
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MN + PQ = MP + NQ.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MNQP là hình thang cân.
cho hai đường tròn o và o tiếp xúc ngoài tại a. kẻ tiếp tuyến chung ngoiaf mn với m thuộc (O) và n thuộc (O'). gọi p là điểm đối xứng với m qua oo', q là điểm đối xứng với n qua oo'.chứng minh
a)mnpq là hình thang cân
b) PQ là tếp tuyến chung của hai đường tròn (O) và (O')
MN + PQ = MP + NQ
cho hai đường tròn o và o tiếp xúc ngoài tại a. kẻ tiếp tuyến chung ngoiaf mn với m thuộc (O) và n thuộc (O'). gọi p là điểm đối xứng với m qua oo', q là điểm đối xứng với n qua oo'.chứng minh
a)mnpq là hình thang cân
b) PQ là tếp tuyến chung của hai đường tròn (O) và (O')
MN + PQ = MP + NQ
Giải bài :Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Gọi P là điểm đối xứng với M qua OO', Q là điểm đối xứng với N qua OO'. Chứng minh rằng: a/ MNPQ là hình thang cân.
Cho hai đường tròn (O) và(O') tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) tại C, cắt đường tròn (O') tại D
a) Chứng minh \(OC//O'D\)
b) Kẻ tiếp tuyến chung ngoài MN, gọi P, Q lần lượt là các điểm đối xứng với M, N qua OO'. Chứng minh MNQP là hình thang cân và \(MN+PQ=MP+NQ\)
c) Tính góc MAN. Gọi K là giao điểm của AM với (O'). Chứng minh N,O',K thẳng hàng
Cho hai đường tròn (O) và(O') tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) tại C, cắt đường tròn (O') tại D
a) Chứng minh OC//O'D
b) Kẻ tiếp tuyến chung ngoài MN, gọi P, Q lần lượt là các điểm đối xứng với M, N qua OO'. Chứng minh MNQP là hình thang cân và MN+PQ=MP+NQ
c) Tính góc MAN. Gọi K là giao điểm của AM với (O'). Chứng minh N,O',K thẳng hàng
Giải nhanh dùm mk nha, cần gấp !!!
Cho hai đường tròn (O) và(O') tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) tại C, cắt đường tròn (O') tại D
a) Chứng minh OC//O'D
b) Kẻ tiếp tuyến chung ngoài MN, gọi P, Q lần lượt là các điểm đối xứng với M, N qua OO'. Chứng minh MNQP là hình thang cân và MN+PQ=MP+NQ
c) Tính góc MAN. Gọi K là giao điểm của AM với (O'). Chứng minh N,O',K thẳng hàng
Giải nhanh dùm mk nha, cần gấp !!!
Cho hai đường tròn (O) và(O') tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) tại C, cắt đường tròn (O') tại D
a) Chứng minh OC//O'D
b) Kẻ tiếp tuyến chung ngoài MN, gọi P, Q lần lượt là các điểm đối xứng với M, N qua OO'. Chứng minh MNQP là hình thang cân và MN+PQ=MP+NQ
c) Tính góc MAN. Gọi K là giao điểm của AM với (O'). Chứng minh N,O',K thẳng hàng
