\(\sqrt{xy}\le\dfrac{x+y}{2}\Rightarrow\dfrac{1}{\sqrt{xy}}\ge\dfrac{2}{x+y}\)
\(\Rightarrow A\ge\dfrac{1}{x}+\dfrac{2}{x+y}=2\left(\dfrac{1}{2x}+\dfrac{1}{x+y}\right)\ge2.\dfrac{4}{2x+x+y}=\dfrac{8}{3x+y}\ge\dfrac{8}{4}=2\)
\(A_{min}=2\) khi \(x=y=1\)

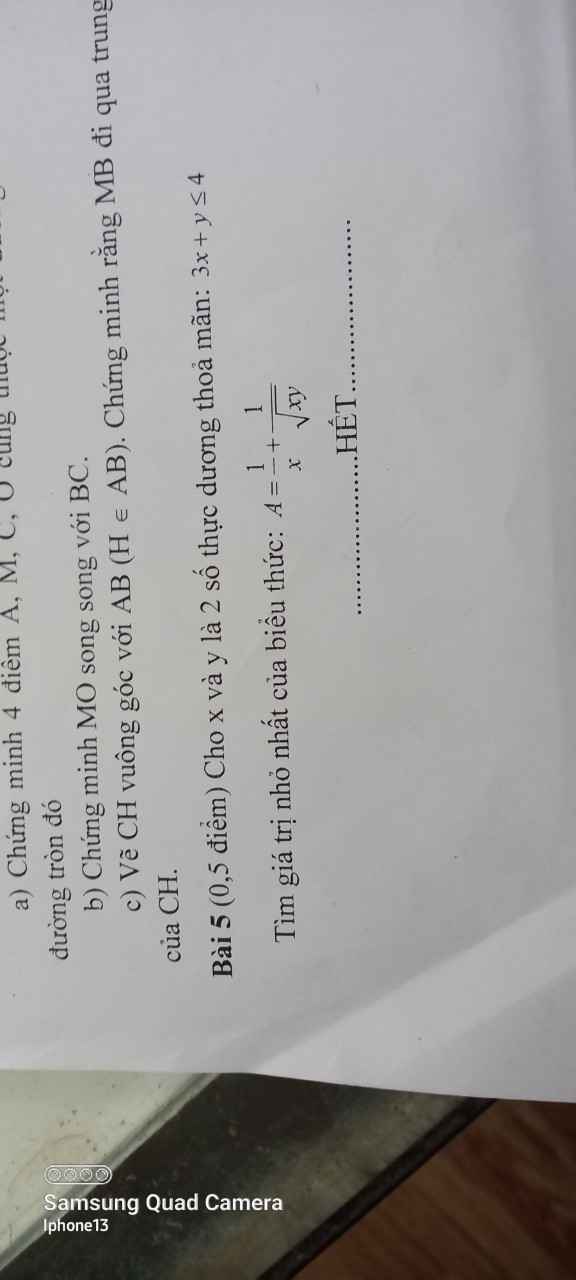





 somebody help me plz =))
somebody help me plz =))






