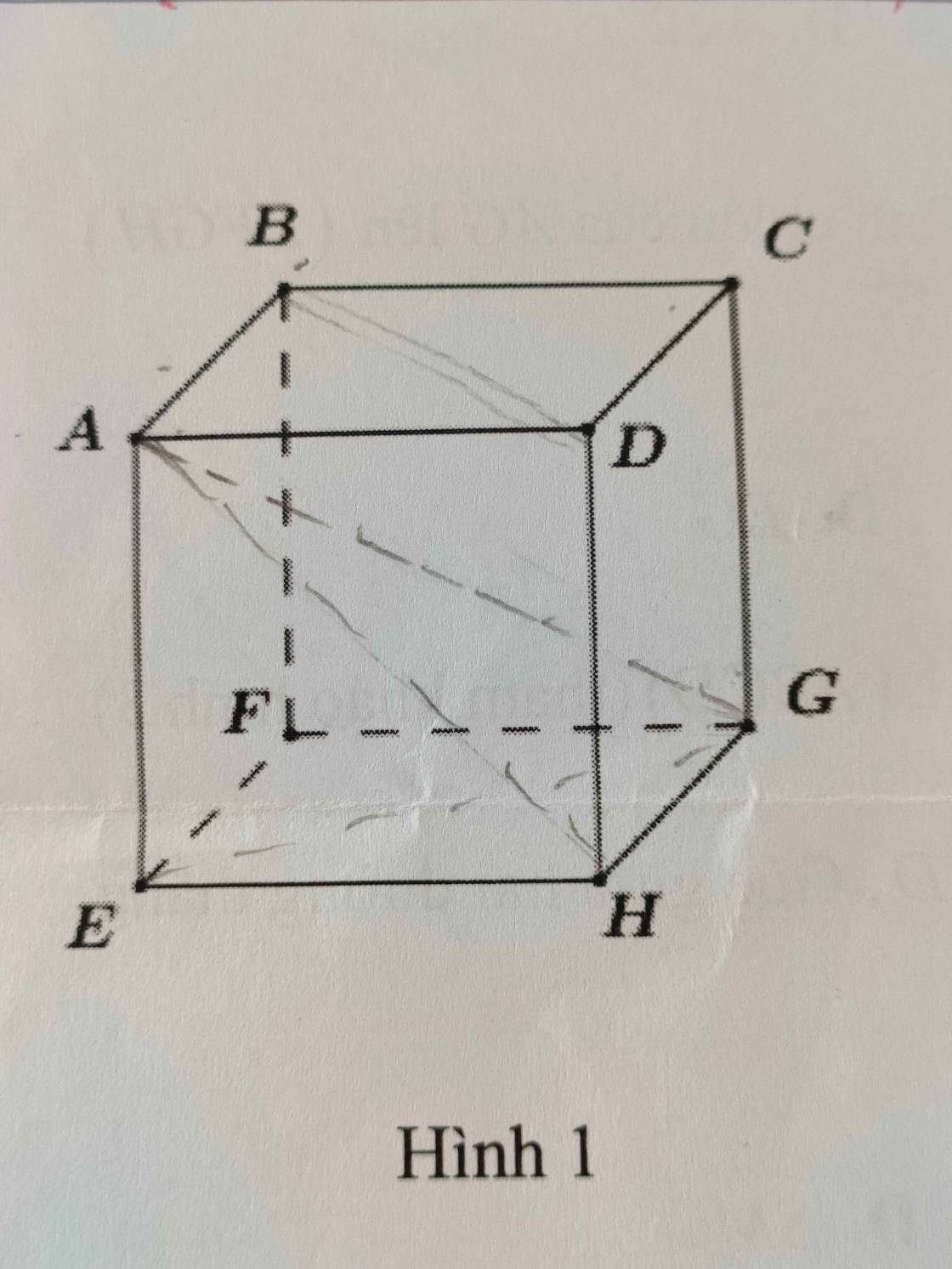
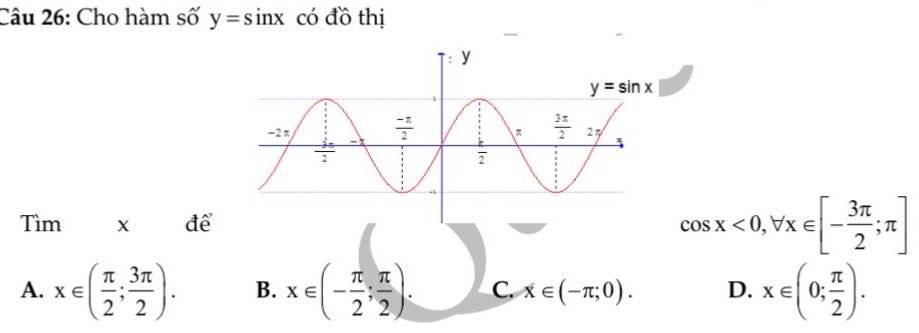
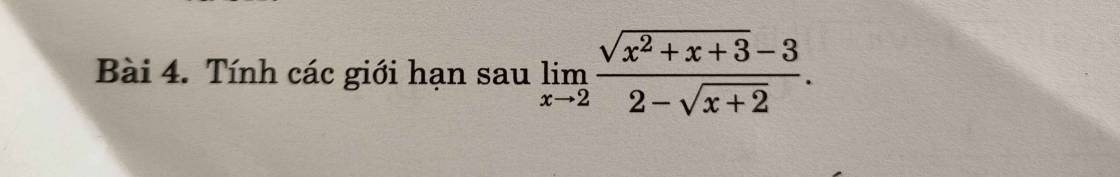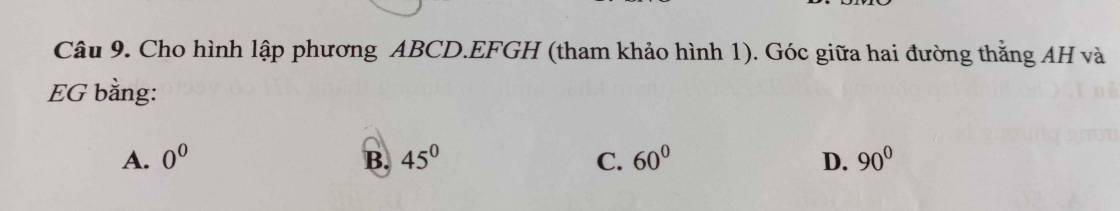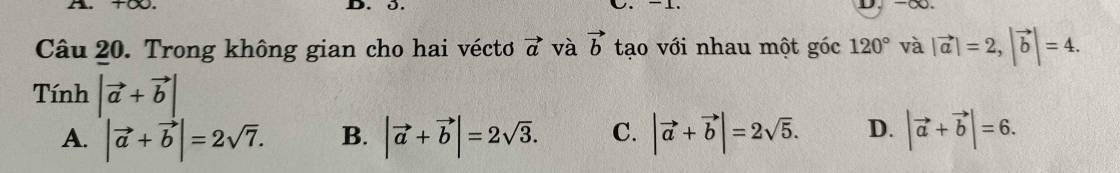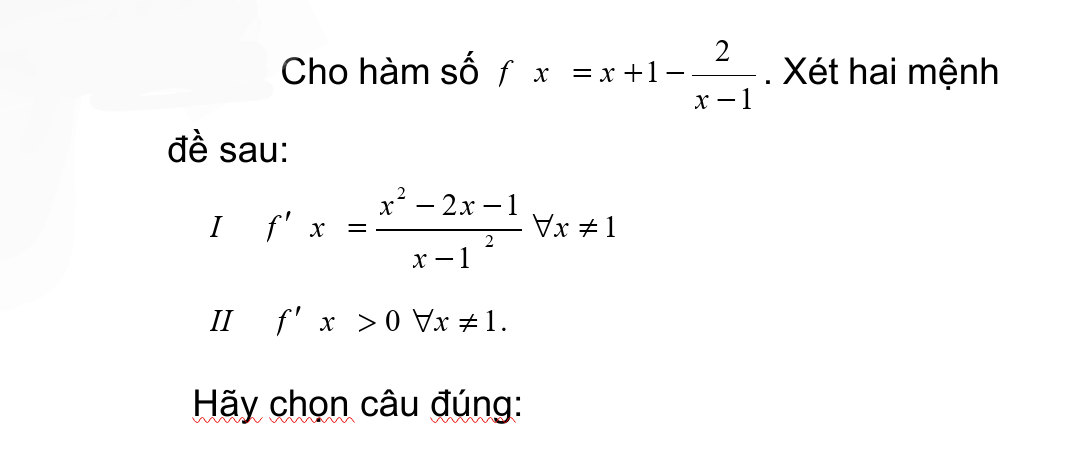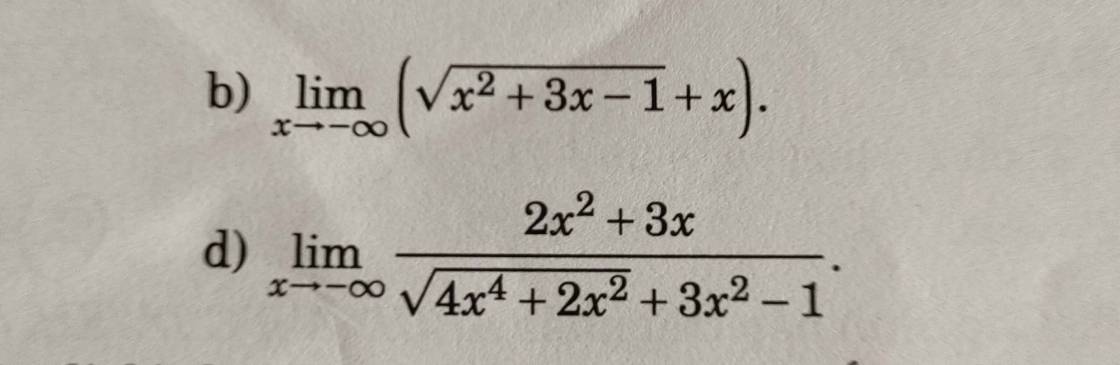giúp mình mấy câu này aaa
```plaintext
(n \in \mathbb{N}^*)
f) \, y = \frac{\sqrt{x}}{x+1}
\text{Tính } y'(2)
g) \, y = (\sqrt{x+1})(x^2+2)
\text{Tính } y(1)
(2x+2)(1-x)
2x - 2x^2 + 2 - 2x
\text{Tính đạo hàm}
a) \, y = 2x(4-x^3)
y' = (2x)'(4-x^3)
= 2(4-x^3) + 2x(-3x^2)
= 8 - 2x^3
b) \, y = 2x^2 + 2x\sqrt{x} + \frac{1}{4}x - 20
c) \, y = \frac{x-1}{2x+3}
d) \, y = \frac{4-3x}{x-1} \quad \rightarrow \, y'(2)
e) \, y = \frac{x^2+2x}{1-x} \quad \rightarrow \, y'(-1)
y' = \frac{(x^2+2x)'(1-x) - (1-x)'(x^2+2x)}{(1-x)^2}
```
a: \(y=2x\left(4-x^3\right)=8x-2x^4\)
=>\(y'=8\cdot1-2\cdot4x^3=-8x^3+8\)
b: \(y=2x^2+2x\sqrt{x}+\dfrac{1}{4}x-20\)
=>\(y=2x^2+2\cdot x^{\dfrac{3}{2}}+\dfrac{1}{4}x-20\)
=>\(y'=2\cdot2x+2\cdot\dfrac{3}{2}\cdot x^{\dfrac{3}{2}-1}+\dfrac{1}{4}\)
=>\(y'=4x+3x^{\dfrac{1}{2}}+\dfrac{1}{4}\)
c: \(y=\dfrac{x-1}{2x+3}\)
=>\(y'=\dfrac{\left(x-1\right)'\cdot\left(2x+3\right)-\left(x-1\right)\left(2x+3\right)'}{\left(2x+3\right)^2}\)
=>\(y'=\dfrac{2x+3-2\left(x-1\right)}{\left(2x+3\right)^2}=\dfrac{5}{\left(2x+3\right)^2}\)
d: \(y=\dfrac{4-3x}{x-1}\)
=>\(y'=\dfrac{\left(-3x+4\right)'\cdot\left(x-1\right)-\left(-3x+4\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
=>\(y'=\dfrac{-3\left(x-1\right)-\left(-3x+4\right)}{\left(x-1\right)^2}=\dfrac{-1}{\left(x-1\right)^2}\)
e: \(y=\dfrac{x^2+2x}{1-x}\)
=>\(y'=\dfrac{\left(x^2+2x\right)'\left(1-x\right)-\left(x^2+2x\right)\left(1-x\right)'}{\left(1-x\right)^2}\)
=>\(y'=\dfrac{\left(2x+2\right)\left(1-x\right)-\left(x^2+2x\right)\cdot\left(-1\right)}{\left(x-1\right)^2}\)
=>\(y'=\dfrac{2x-2x^2+2-2x+x^2+2x}{\left(x-1\right)^2}=\dfrac{-x^2+6x+2}{\left(x-1\right)^2}\)
