Các câu hỏi tương tự
Phương trình (x2−6x)√17−x2=x2−6x(x2−6x)17−x2=x2−6x có bao nhiêu nghiệm phân biệt?
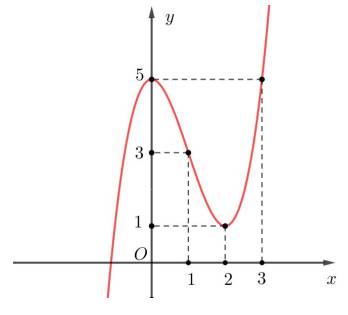
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hỏi phương trình \(f\left(x^3-2x^2+14x+\sqrt{17}\right)=\sqrt{17}\) có bao nhiêu nghiệm thực?
hỏi tất cả có bao nhiêu giá trị để phương trình \(\left(m+1\right)x^2-2\left(m+3\right)x+2m+9=0\) có 2 nghiệm phân biệt
A.5 B.3 C.2 D.4
Giải phương trình sau
1. \(5x^2-16x+7+\left(x+1\right)\sqrt{x^2+3x-1}=0\)
2. \(3\left(\sqrt{2x^2+1}-1\right)=x\left(1+3x+8\sqrt{2x^2+1}\right)\)
\(\left(\frac{2x-1}{2-x}+2\sqrt{2-x}\right)^3=27\left(2x-1\right)\)
Giải phương trình nghiệm nguyên sau:
\(3x^3-13x^2+30x-4=\sqrt{\left(6x+2\right)\left(3x-4\right)^3}\)
tìm m để phương trình 3|x2 - 6x + 5| = 2 - 4m có 4 nghiệm phân biệt
Cho phương trình:\(\left(x^2+3x+2\right)\left(x^2+9x+20\right)-m+1=0\). Tìm các giá trị của m để phương trình có nghiệm thỏa mãn \(x^2+6x+7\le0\)
giải phương trình \(^{^{x^2-25=\left(x^2-6x+25\right)\sqrt{x^2-3x}}}\)
Có bao nhiêu giá trị nguyên của tham số m ∈ [ -2020; 2020 ] thỏa mãn phương trình : \(x^2+\left(2-m\right)x+1=2\sqrt{x^3+x}\) có nghiệm ?
Giải phương trình:
a, \(x^2-6x+9=4\sqrt{x^2-6x+6}\)
b,\(\frac{x^2-4x+4}{x^2-2x+1}+\frac{\left|2x-4\right|}{\left|x-1\right|}=3\)










