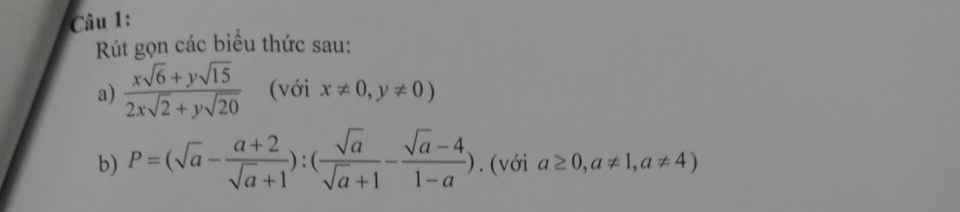Ta có : x3 + y3 + 3(x2y + xy2) = 35 + 3.30
<=> (x + y)3 = 125
<=> x + y = 5 (1)
mà x2y + xy2 = 30
<=> xy(x + y) = 30
<=> xy = 6
Từ (1) => (x + y)2 = 25
<=> x2 + y2 + 2xy = 25
<=> x2 + y2 - 2xy = 1
<=> (x - y)2 = 1
<=> x - y = \(\pm1\)
Khi x - y = 1 ; x + y = 5 => x = 3 ; y = 2
Khi x - y = -1 ; x + y = 5 => x = 2 ; y = 3
8) \(\hept{\begin{cases}x^2y+xy^2=30\\x^3+y^3=35\end{cases}}\Leftrightarrow\hept{\begin{cases}xy\left(x+y\right)=30\\\left(x+y\right)^3-3xy\left(x+y\right)=35\end{cases}}\)
Đặt xy = a ; x + y = b , hpt đã cho trở thành \(\hept{\begin{cases}ab=30\\b^3-3ab=35\end{cases}}\Leftrightarrow\hept{\begin{cases}ab=30\\b^3-90=35\end{cases}}\Leftrightarrow\hept{\begin{cases}ab=30\\b^3=125\end{cases}}\Leftrightarrow\hept{\begin{cases}ab=30\\b=5\end{cases}}\Leftrightarrow\hept{\begin{cases}a=6\\b=5\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=5\\xy=6\end{cases}}\). Đến đây bạn giải pt x2 - Sx+ P = 0 với S = x + y và P = xy nhé , trong SGK có hd đấy:)
=> x = 2 ; y = 3 hoặc x = 3 ; y = 2
9) ĐK : x,y khác 0
\(\hept{\begin{cases}\left(x+y\right)\left(1+\frac{1}{xy}\right)=5\\\left(x^2+y^2\right)\left(1+\frac{1}{x^2y^2}\right)=49\end{cases}}\Leftrightarrow\hept{\begin{cases}x+\frac{1}{x}+y+\frac{1}{y}=5\\x^2+\frac{1}{x^2}+y^2+\frac{1}{y^2}=49\end{cases}}\)(1)
Đặt \(\hept{\begin{cases}x+\frac{1}{x}=a\\y+\frac{1}{y}=b\end{cases}}\left(a,b\ne0\right)\Rightarrow\hept{\begin{cases}x^2+\frac{1}{x^2}=a^2-2\\y^2+\frac{1}{y^2}=b^2-2\end{cases}}\)
Khi đó \(\left(1\right)\Leftrightarrow\hept{\begin{cases}a+b=5\\a^2+b^2-4=49\end{cases}}\Leftrightarrow\hept{\begin{cases}a=5-b\\\left(5-b\right)^2+b^2-53=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=5-b\\b^2-5b-14=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=5-b\\\left(b-7\right)\left(b+2\right)=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=5-b\\b=7hoacb=-2\end{cases}\Leftrightarrow}\hept{\begin{cases}a=-2\\b=7\end{cases}\left(tm\right)hoac\hept{\begin{cases}a=7\\b=-2\end{cases}\left(tm\right)}}\)
ơ ơ ngu ngơ chưa gì đã ấn nộp bài:( làm tiếp :v
TH1 : a = -2 ; b = 7 => \(\hept{\begin{cases}x+\frac{1}{x}=-2\\y+\frac{1}{y}=7\end{cases}}\)bạn tự giải tiếp:) => \(\hept{\begin{cases}x=-1\\y=\frac{7\pm3\sqrt{5}}{2}\end{cases}}\)(tm)
TH2 : a = 7 ; b = -2 => \(\hept{\begin{cases}x+\frac{1}{x}=7\\y+\frac{1}{y}=-2\end{cases}}\)tương tự => \(\hept{\begin{cases}x=\frac{7\pm3\sqrt{5}}{2}\\y=-1\end{cases}\left(tm\right)}\)
Vậy ...
10) \(\hept{\begin{cases}x+y-2xy=5\\x^2+y^2-xy=7\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y-2xy=5\\\left(x+y\right)^2-3xy=7\end{cases}}\)
Đặt x + y = a ; xy = b , hpt đã cho trở thành \(\hept{\begin{cases}a-2b=5\\a^2-3b=7\end{cases}}\Leftrightarrow\hept{\begin{cases}-\frac{3}{2}a+3b=-\frac{15}{2}\\a^2-3b=7\end{cases}}\Leftrightarrow\hept{\begin{cases}-\frac{3}{2}a+3b=-\frac{15}{2}\\a^2-\frac{3}{2}a+\frac{1}{2}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}-\frac{3}{2}a+3b=-\frac{15}{2}\\2a^2-3a+1=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-\frac{3}{2}a+3b=-\frac{15}{2}\\\left(a-1\right)\left(2a-1\right)=0\end{cases}}\Leftrightarrow\hept{\begin{cases}-\frac{3}{2}a+3b=-\frac{15}{2}\\a=1hoaca=\frac{1}{2}\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=-2\end{cases}hoac\hept{\begin{cases}a=\frac{1}{2}\\b=-\frac{9}{4}\end{cases}}}\)
TH1 : a = 1 ; b = -2 => \(\hept{\begin{cases}x+y=1\\xy=-2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}hoac\hept{\begin{cases}x=2\\y=-1\end{cases}}}\)
TH2 : a = 1/2 ; b = -9/4 \(\Rightarrow\hept{\begin{cases}x+y=\frac{1}{2}\\xy=-\frac{9}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1+\sqrt{37}}{4}\\y=\frac{1-\sqrt{37}}{4}\end{cases}}hoac\hept{\begin{cases}x=\frac{1-\sqrt{37}}{4}\\\frac{1+\sqrt{37}}{4}\end{cases}}\)