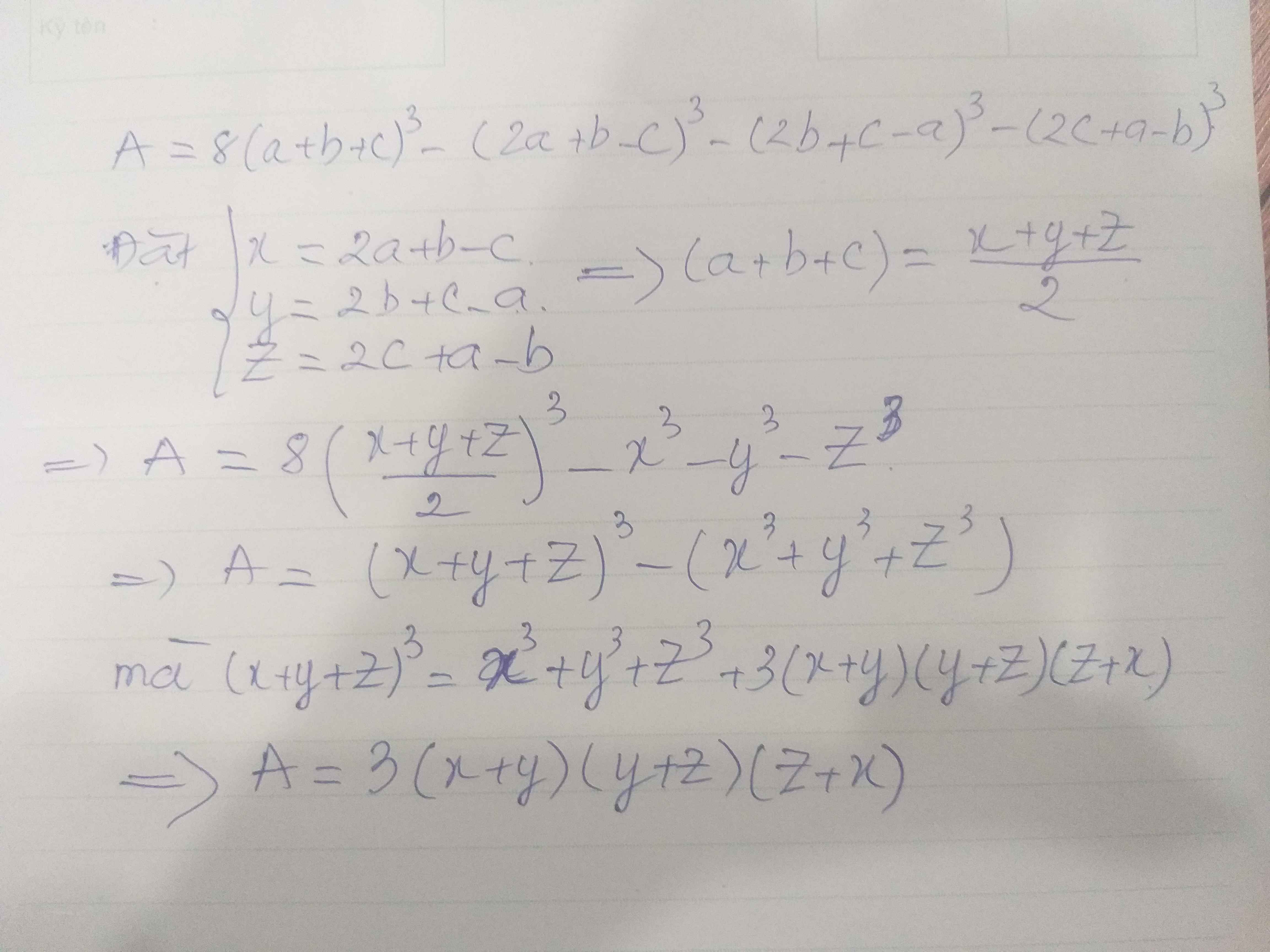Đặt 2a+b-c=x; 2b+c-a=y; 2c+a-b=z
=>x+y+z=2a+2b+2c=2(a+b+c)
\(A=8\left(a+b+c\right)^3-\left(2a+b-c\right)^3-\left(2b+c-a\right)^3-\left(2c+a-b\right)^3\)
\(=\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left(x+y+z-x\right)\left[\left(x+y+z\right)^2+x\left(x+y+z\right)+x^2\right]-\left(y+z\right)\left(y^2-yz+z^2\right)\)
\(=\left(y+z\right)\left[x^2+y^2+z^2+2xy+2yz+2xz+x^2+xy+xz+x^2-y^2+yz-z^2\right]\)
=(y+z)\(\left(3x^2+3xy+3yz+3xz\right)\)
\(=3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(=3\left(2a+b-c+2b+c-a\right)\left(2a+b-c+2c+a-b\right)\left(2b+c-a+2c+a-b\right)\)
=3(a+3b)(3a+c)(b+3c)
Đúng 1
Bình luận (0)
