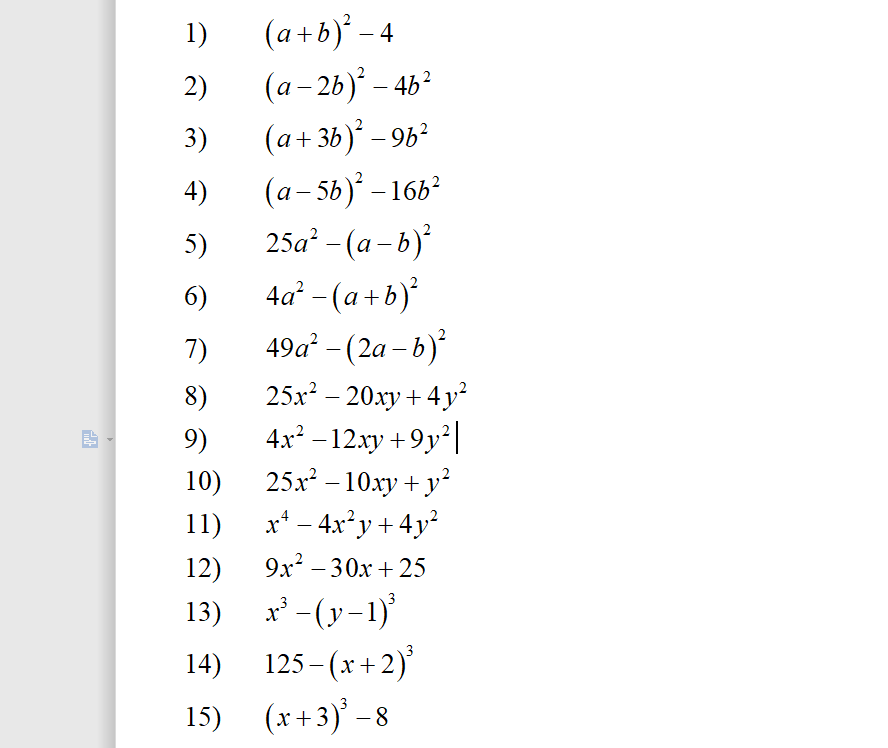
`x^16 + x^8 + 1`
`= x^16 + 2x^8 + 1 - x^8`
`= (x^8 + 1)^2 - (x^4)^2`
`= (x^8 - x^4 + 1)(x^8 + x^4 + 1) `
`= (x^8 - x^4 + 1)[(x^8 + 2x^4 + 1) - x^4]`
`= (x^8 - x^4 + 1)[(x^4 + 1)^2 - (x^2)^2]`
`= (x^8 - x^4 + 1)(x^4 + 1 -x^2) (x^4 + 1+ x^2) `
`= (x^8 - x^4 + 1)(x^4 + 1 -x^2)[ (x^4 + 1+ 2x^2) - x^2] `
`= (x^8 - x^4 + 1)(x^4 + 1 -x^2)[ (x^2 + 1)^2 - x^2] `
`= (x^8 - x^4 + 1)(x^4 + 1 -x^2)(x^2 -x + 1)(x^2 + x + 1)`
10: \(I=4x^4y^4+1\)
\(=4x^4y^4+4x^2y^2+1-4x^2y^2\)
\(=\left(2x^2y^2+1\right)^2-\left(2xy\right)^2\)
\(=\left(2x^2y^2+2xy+1\right)\left(2x^2y^2-2xy+1\right)\)
11: \(M=4\left(x^2-y^2\right)-8\left(x-ay\right)-4\left(a^2-1\right)\)
\(=4\left(x^2-y^2-2x+2ay-a^2+1\right)\)
\(=4\left[\left(x^2-2x+1\right)-\left(y^2-2ay+a^2\right)\right]\)
\(=4\left[\left(x-1\right)^2-\left(y-a\right)^2\right]\)
\(=4\left(x-1-y+a\right)\left(x-1+y-a\right)\)
12: \(N=\left(x^2-7x+12\right)\left(x^2-15x+56\right)-60\)
\(=\left(x-3\right)\left(x-4\right)\left(x-7\right)\left(x-8\right)-60\)
\(=\left(x^2-11x+24\right)\left(x^2-11x+28\right)-60\)
\(=\left(x^2-11x\right)^2+52\left(x^2-11x\right)+24\cdot28-60\)
\(=\left(x^2-11x\right)^2+52\left(x^2-11x\right)+612\)
\(=\left(x^2-11x+18\right)\left(x^2-11x+34\right)\)
\(=\left(x-9\right)\left(x-2\right)\left(x^2-11x+34\right)\)
13: Đặt \(x^2+x+1=a;x-1=b\)
=>\(a\cdot b=\left(x^2+x+1\right)\left(x-1\right)=x^3-1\)
\(P=2\left(x^2+x+1\right)^2-7\left(x-1\right)^2-13\left(x^3-1\right)\)
\(=2a^2-7b^2-13ab\)
\(=2a^2-14ab+ab-7b^2\)
\(=2a\left(a-7b\right)+b\left(a-7b\right)\)
\(=\left(a-7b\right)\left(2a+b\right)\)
\(=\left(x^2+x+1-7x+7\right)\left(2x^2+2x+2+x-1\right)\)
\(=\left(x^2-6x+8\right)\left(2x^2+3x+1\right)\)
\(=\left(x-2\right)\left(x-4\right)\left(2x+1\right)\left(x+1\right)\)
15: \(R=x^4+2000x^2+1999x+2000\)
\(=x^4+x^3+x^2-x^3-x^2-x+2000x^2+2000x+2000\)
\(=x^2\left(x^2+x+1\right)-x\left(x^2+x+1\right)+2000\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2000\right)\)
`x^8 + x^7 + 1`
`= x^8 +x^7 + x^6 - x^6 + 1`
`= x^6 (x^2 + x + 1) - (x^6 - 1)`
`= x^6 (x^2 + x + 1) - ((x^3)^2 - 1^2)`
`= x^6 (x^2 + x + 1) - (x^3 - 1)(x^3 + 1)`
`= x^6 (x^2 + x + 1) - (x - 1)(x^2 + x + 1)(x+1)(x^2 - x +1)`
`= (x^2 + x +1) . [x^6 - (x - 1)(x+1)(x^2 - x +1)]`
`= (x^2 + x +1) . [x^6 - (x - 1)(x^3 + 1)]`
`= (x^2 + x +1) . [x^6 - (x^4 - x^2 + x - 1)]`
`= (x^2 + x +1) . (x^6 - x^4 + x^2 - x + 1)`
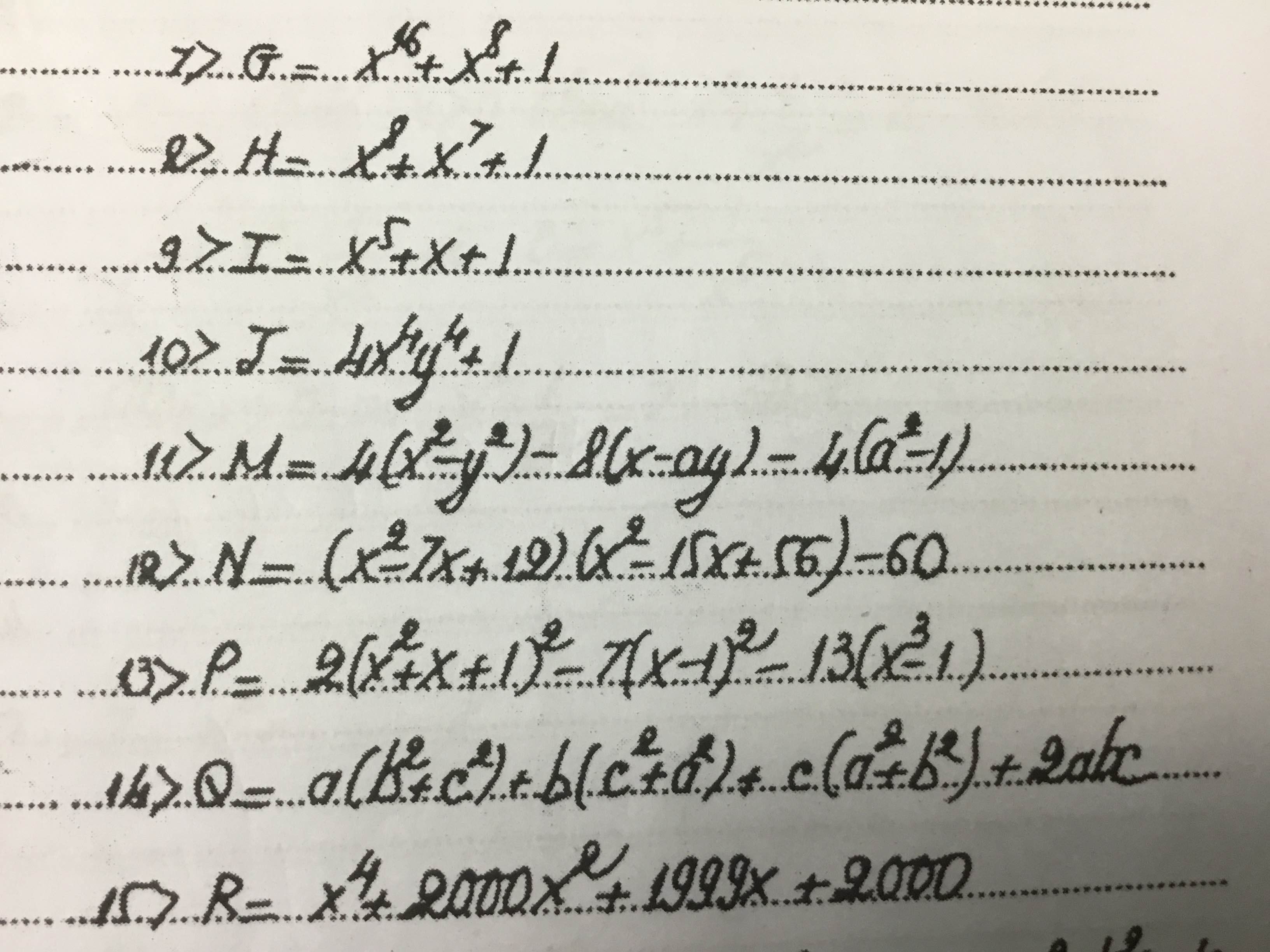
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)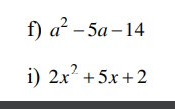
phân tích đa thức sau thành nhân tử(tách 1 hạng tử 
